量子プログラミングについて少しずつ分かってきたので、もう少しステップを進めていきたい。
自作の量子コンピュータ・シミュレータの拡張を考えるためにも、GoogleやMicrosoftが発表している量子コンピュータのフレームワークについて勉強し、そこでいろいろな量子プログラミングの手法を勉強すべきだろう。
という訳で、まずはGoogleの量子コンピュータフレームワークであるcirqを使ってみることにした。 試してみたのは、もちろん全加算器(1-bit)からだ。
Google Cirqのチュートリアル
Google Cirqのチュートリアルは以下で公開されている。
- Tutorial : Google Cirq
Tutorial — Cirq 0.1 documentation
これによると、基本的な考え方は自作シミュレータで培ったものと同じで、少し違うのはグリッドというものに拡張されていることだ。 グリッドといっても、2次元であるだけで別に1次元で考えても大して変わらない。
まずは、このグリッドを使って4つの量子ビットを定義する。
qbits = [cirq.GridQubit(0, i) for i in range(4)]
次に、量子回路を作って全加算器を構成する。単純だ。
circuit = cirq.Circuit() circuit.append(cirq.CCX.on(qbits[0], qbits[1], qbits[3])) circuit.append(cirq.CNOT.on(qbits[0], qbits[1])) circuit.append(cirq.CCX.on(qbits[1], qbits[2], qbits[3])) circuit.append(cirq.CNOT.on(qbits[1], qbits[2])) circuit.append(cirq.CNOT.on(qbits[0], qbits[1])) print(circuit)
以下のようなグラフが出力された。正しく構成できていると思う。
全加算器のシミュレーションをする
全加算器のシミュレーションをするためには、最初の量子ビットの状態(qbits[0]とqbits[1]の値)を変更したいのだが、どうもその方法が分からない。
仕方がないので、量子ビットの先頭に反転ゲートを挿入して、それっぽく動作させることにした。
つまり、 を実行したければ、aが格納されている量子ビット
qbits[0]を最初に反転させるわけだ。
... circuit = cirq.Circuit() # circuit.append(cirq.X(qbits[0])) # Set initial value of a # circuit.append(cirq.X(qbits[1])) # Set initial value of b circuit.append(cirq.CCX.on(qbits[0], qbits[1], qbits[3])) circuit.append(cirq.CNOT.on(qbits[0], qbits[1])) circuit.append(cirq.CCX.on(qbits[1], qbits[2], qbits[3]))
次にシミュレーションを行う。最後に結果を観測するために観測器を取り付けた。measureがそれに当たる。
simulator = cirq.google.XmonSimulator() circuit.append(cirq.measure(qbits[2], key='s')) circuit.append(cirq.measure(qbits[3], key='c')) print(circuit) results = simulator.run(circuit, repetitions=100, qubit_order=qbits) print (results.histogram(key='s')) print (results.histogram(key='c'))
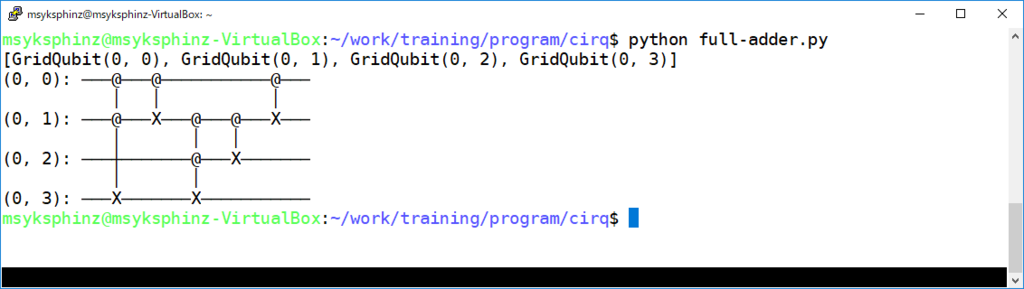
実行すると以下のようになった。
$ python full-adder.py [GridQubit(0, 0), GridQubit(0, 1), GridQubit(0, 2), GridQubit(0, 3)] (0, 0): ───@───@───────────@─── │ │ │ (0, 1): ───@───X───@───@───X─── │ │ │ (0, 2): ───┼───────@───X─────── │ │ (0, 3): ───X───────X─────────── (0, 0): ───@───@───────────@───────────────────── │ │ │ (0, 1): ───@───X───@───@───X───────────────────── │ │ │ (0, 2): ───┼───────@───X───────M('s')──────────── │ │ (0, 3): ───X───────X────────────────────M('c')─── Counter({0: 100}) Counter({0: 100})
最後に、qbits[2]の値(=s)が0、qbits[3]の値(=c)が0となっている。
厳密には、100回シミュレーションしてそれぞれのビットが0となっている回数が100回(つまり全部)となった。
たとえば、上記のコメントを外してを実行してみる。
[GridQubit(0, 0), GridQubit(0, 1), GridQubit(0, 2), GridQubit(0, 3)] (0, 0): ───X───────@───@───────────@─── │ │ │ (0, 1): ───────X───@───X───@───@───X─── │ │ │ (0, 2): ───────────┼───────@───X─────── │ │ (0, 3): ───────────X───────X─────────── (0, 0): ───X───────@───@───────────@───────────────────── │ │ │ (0, 1): ───────X───@───X───@───@───X───────────────────── │ │ │ (0, 2): ───────────┼───────@───X───────M('s')──────────── │ │ (0, 3): ───────────X───────X────────────────────M('c')─── Counter({0: 100}) Counter({1: 100})
この場合は、s=0, c=1となっているのキャリーが発生している。正しく動作したようだ。
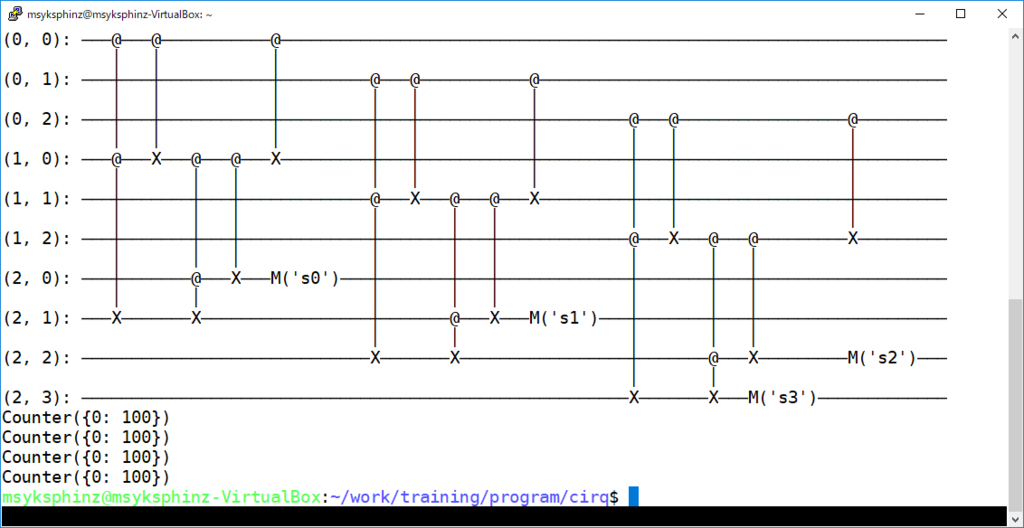
ちなみに、3ビットの加算器だと以下のようになる。まだテストしてないけど。