RVA23で追加されている、Zfh拡張及びZfhmin拡張について調べている。ドキュメントを読みながら、まとめていこう。
これらはIEEE 754-2008規格に準拠した16ビット半精度浮動小数点命令を提供する拡張である。
Zfh拡張の概要
Zfh拡張は、16ビット半精度浮動小数点(half-precision)命令を追加するものであり、単精度浮動小数点拡張(F拡張)に依存している。 NaN Boxing化の仕組みも拡張され、半精度値を単精度値内にNaN Boxing化できる(さらにD拡張やQ拡張があれば、倍精度・4倍精度にも再帰的にNaN Boxing化可能である)。
この拡張は主に、半精度オペランドを取り、半精度の結果を生成する命令を定義する。 ただし、計算自体はより高い精度で行い、結果のみ半精度に変換するパターンも一般的である。 Zfh拡張には明示的な変換命令が含まれており、将来的にはさらに効率的な命令が追加される可能性がある。
半精度ロード・ストア命令
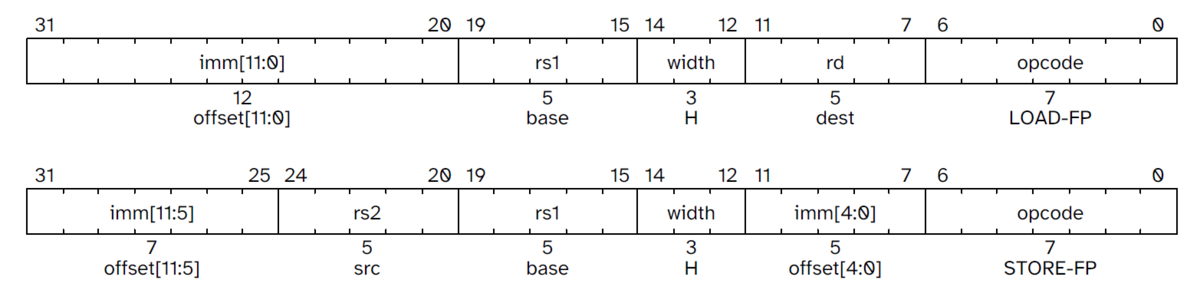
LOAD-FPおよびSTORE-FP命令に16ビット幅のバリアント(FLH, FSH)が追加されている。
これらは新たなfunct3幅フィールド値でエンコードされる。
FLH: 半精度浮動小数点値をロードし、rdにNaN Boxing化して格納する。FSH: rs2の下位16ビットのみをストアする。
FLH/FSHは、アドレスが自然アラインされている場合のみアトミックに実行されることが保証される。
NaNのペイロードも保持される。
半精度算術演算命令
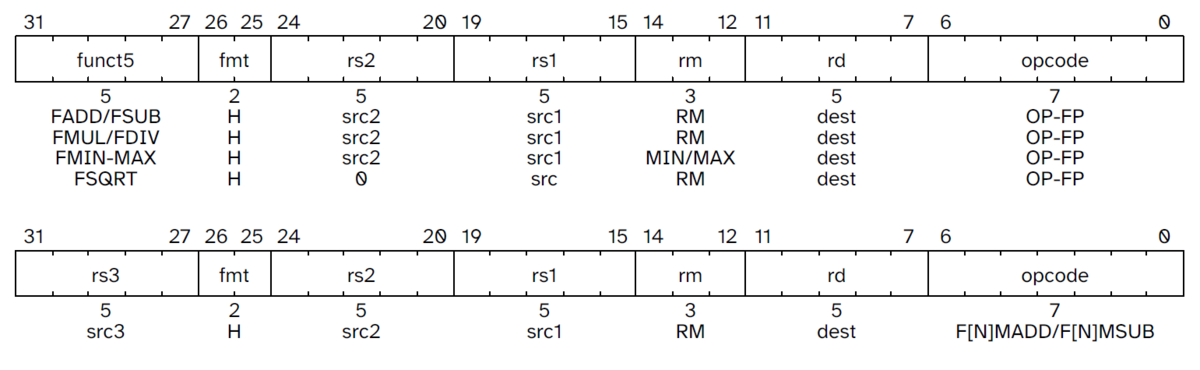
多くの浮動小数点命令に新たなフォーマット(fmt=10, H)が追加され、半精度オペランド・結果に対応する。
FADD.H,FSUB.H,FMUL.H,FDIV.H,FSQRT.H: 半精度で加減乗除・平方根を行う。FMIN.H,FMAX.H: 半精度で最小・最大値を求める。F[N]MADD.H,F[N]MSUB.H: 半精度で積和・積差を求める。
半精度変換・移動命令
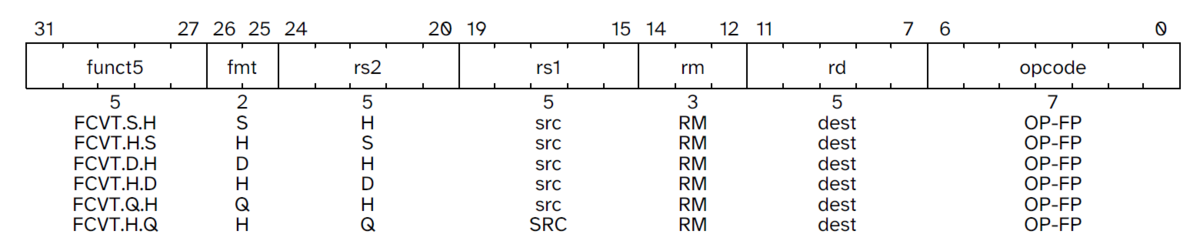
FCVT.W.H / FCVT.L.H: 半精度→32/64ビット符号付き整数へ変換。FCVT.H.W / FCVT.H.L: 32/64ビット符号付き整数→半精度へ変換。FCVT.WU.H / FCVT.LU.H / FCVT.H.WU / FCVT.H.LU: 符号なし整数との相互変換。FCVT.S.H / FCVT.H.S: 半精度と単精度間の変換。FCVT.D.H / FCVT.H.D: 半精度と倍精度間の変換(D拡張がある場合)。FCVT.Q.H / FCVT.H.Q: 半精度と4倍精度間の変換(Q拡張がある場合)。FSGNJ.H, FSGNJN.H, FSGNJX.H: 半精度の符号付け操作。FMV.X.H / FMV.H.X: 浮動小数点レジスタと整数レジスタ間でビットパターンを移動。


半精度比較命令
FEQ.H, FLT.H, FLE.H: 半精度オペランドでの比較命令。

半精度クラス判定命令
FCLASS.H: 半精度値のクラス(正の無限大、NaNなど)を判定。

Zfhmin拡張: 最小限の半精度浮動小数点サポート
Zfhmin拡張は、Zfh拡張のサブセットであり、データ転送と変換命令のみを定義する。 主にストレージ用途で半精度を使い、計算はより高精度で行うことを想定している。
Zfhminに含まれる命令は以下の通りである:
- FLH, FSH
- FMV.X.H, FMV.H.X
- FCVT.S.H, FCVT.H.S
- (D拡張があれば)FCVT.D.H, FCVT.H.D
- (Q拡張があれば)FCVT.Q.H, FCVT.H.Q
なお、 FSGNJ.H 命令は含まれないが、 FSGNJ.S 命令で代用可能である。
エミュレーションについて
半精度の加減乗除・平方根演算は、オペランドを単精度に変換し、単精度演算後に半精度へ戻すことで忠実にエミュレートできる。 積和演算(FMA)は一部の丸めモードで1ULPの誤差が生じる場合がある。
8/16ビット整数から半精度への変換は、まず単精度へ変換し、その後半精度へ変換することでエミュレートできる 。32ビット整数の場合は倍精度を経由するのが正確だが、D拡張がない場合や1ULP誤差が許容できる場合は単精度経由でもよい。 同様に、64ビット整数からの変換もQ拡張がなければ単精度経由で近似できる。