Microsoft Q# Programmingのガイドには、最初のサンプルプログラムとして量子テレポーテーションが登場している。
これは量子回路で表現すると、以下のようになっている。うん、訳が分からん。
色々と資料を読みながら、量子テレポーテーションについて勉強していこう。
- Quantum Teleportation
https://www.appi.keio.ac.jp/Itoh_group/abe/pdf/qc2.pdf
- 量子コンピュータ授業 #2 量子テレポーテーション
https://www.youtube.com/watch?v=mose-W49uF8&index=2&list=PLB1324F2305C028F7
そもそも量子テレポーテーションとは
- 量子アルゴリズムという程ではないけれども、最も重要な量子の操作の一つ。
- 量子コンピュータにおいて、データを転送する (たとえその量子ビットが遠く離れていても)。
- エンタングルメント状態を活用することで実現できる。
量子ビットの状態を知ることなく、転送することができる!
Alice, Bob, Victorという3人がいる。
- AliceとBobが量子の状態をエンコードしておき、AliceとVictorがデコードすることで、Bobの状態を知ることができる。
2つの量子ビットがあり、AliceとBobがそれぞれ保持している。
- VictorとAliceのベル状態のペアを作成する。
- Aliceの測定により、Bell Pairは
つの状態に確定する。
- → Bobの状態は、Victorのもともとの状態に近い状態になっている。
- → Aliceはクラシカルな方法で、BobにAliceの状態を伝える。
- → BobはXをかけることにより、Bobは自分の状態を知ることができる。
- Aliceの測定により、Bell Pairは
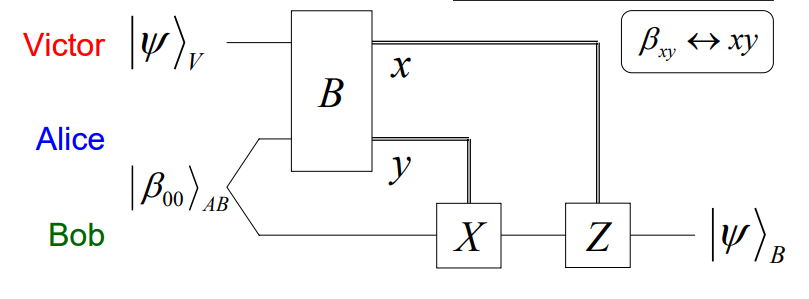
Q#プログラミング言語による実装
こう考えてみると、Q#での実装は量子回路をそのまま実装してあるに過ぎない。
operation Teleport(msg : Qubit, there : Qubit) : () {
body {
using (register = Qubit[1]) {
// Ask for an auxillary qubit that we can use to prepare
// for teleportation.
let here = register[0];
// Create some entanglement that we can use to send our message.
H(here);
CNOT(here, there);
// Move our message into the entangled pair.
CNOT(msg, here);
H(msg);
// Measure out the entanglement.
if (M(msg) == One) { Z(there); }
if (M(here) == One) { X(there); }
// Reset our "here" qubit before releasing it.
Reset(here);
}
}
}

補足. 量子テレポーテーションの理解にあたり必要な量子回路の変換
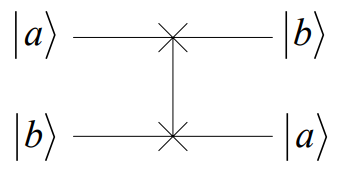
1. 量子状態のSWAP
2つの量子状態の交換は、SWAP操作と呼ばれる (参考資料 : https://www.appi.keio.ac.jp/Itoh_group/abe/pdf/qc1.pdf)
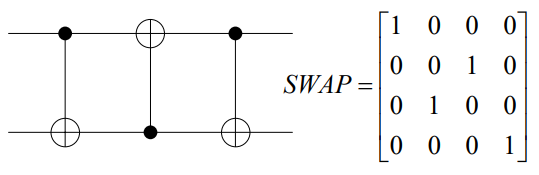
これは、量子ゲートのCNOTを3回組み合わせることで実現できる。
証明
$$\left|a\right>\left|b\right>\rightarrow C_{12}\rightarrow \left|a\right>\left|b\oplus a\right>$$
$$\left|a\right>\left|b\oplus a\right> \rightarrow C_{21}\rightarrow \left|a\oplus(b\oplus a)\right>\left|b\oplus a\right> = \left|b\right>\left|b\oplus a\right>$$
$$\left|b\right>\left|b\oplus a\right> \rightarrow C_{12}\rightarrow \left|b\right>\left|(b\oplus a)\oplus b\right> = \left|b \right>\left|a \right>$$
を
に交換することができた。
2. 3量子ビットのCNOTを、4つのCNOTに変換する
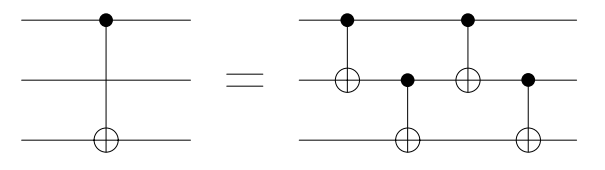
証明
$$\left|a\right>\left|b\right>\left|c\right>\rightarrow C_{12}\rightarrow \left|a\right>\left|(b\oplus a)\right>\left|c\right>$$
$$\left|a\right>\left|(b\oplus a)\right>\left|c\right>\rightarrow C_{23}\rightarrow \left|a\right>\left|(b\oplus a)\right>\left|c\oplus (b\oplus a)\right>$$
$$\left|a\right>\left|(b\oplus a)\right>\left|c\oplus (b\oplus a)\right>\rightarrow C_{12}\rightarrow \left|a\right>\left|(b\oplus a)\oplus a\right>\left|c\oplus (b\oplus a)\right> = \left|a\right>\left|b\right>\left|c\oplus (b\oplus a)\right> $$
$$\left|a\right>\left|b\right>\left|c\oplus (b\oplus a)\right> \rightarrow C_{23}\rightarrow \left|a\right>\left|b\right>\left|c\oplus (b\oplus a)\oplus b\right> = \left|a\right>\left|b\right>\left|c\oplus a\right>$$
これで、 と
の状態のCNOTをとることができた。
