\TensorFlowを使って、サンプル値からの多項式フィッティングを実装してみよう。
参考にした例題は、以下の本に載っている最小二乗法の例だ。以下の本では、sin(2πx)+0.3の関数から10個のサンプルポイントを抽出し、0次多項式から10次多項式まで最小二乗法でフィッティングを行っている。また、その中で、10次でフィッティングさせるとオーバーフィッティングになることも見ている。

- 作者: 中井悦司
- 出版社/メーカー: 技術評論社
- 発売日: 2015/10/17
- メディア: 単行本(ソフトカバー)
- この商品を含むブログを見る
では、同じことをTensorFlowで実現するためにはどのようにすれば良いのだろうか。ここでは、以下のフローを取ってみた。
サンプル点を作成する。
ここでは、上記の書籍と同様に、三角関数を多項式(3次元多項式)にフィッティングさせてみよう。 ここでは、まず100個のサンプルポイントを作成する。
の式に基いて、(x, y)のサンプルのペアを作成する。また、フィッティングをより難しくするために、0.3のバイアスもランダムに上下させ、本物の三角関数にすぐにはフィッティングできないようにしてみる。
x_data = np.float32(np.random.rand(100)) # Random input y_data = np.sin(2*np.pi*x_data) + 0.3 * np.random.rand()
多項式をモデル化する
ここでは、3次の多項式にフィッティングさせてみよう。この場合、4つの変数について最適値を探索する必要があるため、以下のような変数をTensorFlow上で作成する。
W3 = tf.Variable(random.random()) W2 = tf.Variable(random.random()) W1 = tf.Variable(random.random()) W0 = tf.Variable(random.random())
random()を設定しているのは、実際にはこのVariableは初期値が必要だからだ。
http://tensorflow.org/api_docs/python/state_ops.html#Variable
次にこれらの変数を利用して、3次多項式をモデル化してみよう。
y4 = W3*x_data*x_data*x_data+W2*x_data*x_data + W1*x_data + W0
多項式とサンプル点から誤差関数を作成する
これはチュートリアルの受け売りだが、以下のようにしてベクトル列からの誤差関数を作成する。
loss = tf.reduce_mean(tf.square(y4 - y_data))
optimizer = tf.train.GradientDescentOptimizer(0.5)
train = optimizer.minimize(loss)
関数y4とy_dataの差分から、これを誤差関数とし、これを降下法を使って最小化する訳だ。
誤差関数を最小化する
では、トレーニングさせてみる。
# For initializing the variables. init = tf.initialize_all_variables() # Launch the graph sess = tf.Session() sess.run(init) # Fit the plane. for step in xrange(0, 5000): sess.run(train) print step, sess.run(W3), sess.run(W2), sess.run(W1), sess.run(W0)
実行結果は以下のようになった。
python sample.py I tensorflow/core/common_runtime/local_device.cc:25] Local device intra op parallelism threads: 1 I tensorflow/core/common_runtime/local_session.cc:45] Local session inter op parallelism threads: 1 4999 9.17582 -12.8354 2.60596 0.827357
つまり、 [tex:{ 9.17x3-12.83x2+2.60x+0.8273 }] がフィッティングの関数として得られたことになる。
Excelでグラフを書いてみると以下のようになる。

いいね、ちゃんとフィッティングしてくれた。
疑問: 学習するのに時間がかかりや過ぎてないか?
今回は、トレーニングのために5000回もフローを流している。通常、100個のサンプル点であれば、100個のトレーニングデータからある程度フィッティングできるのではないかと予想したが、ずいぶんと学習してくれなかった。最小二乗法の例だと10個の点で十分学習しているのにな。これはアルゴリズムの違い?
学習回数を100回に減らしてみると、以下のようになり全くフィッティングしていなかった。
python sample.py I tensorflow/core/common_runtime/local_device.cc:25] Local device intra op parallelism threads: 1 I tensorflow/core/common_runtime/local_session.cc:45] Local session inter op parallelism threads: 1 99 0.590841 -0.767034 -1.44215 0.95163
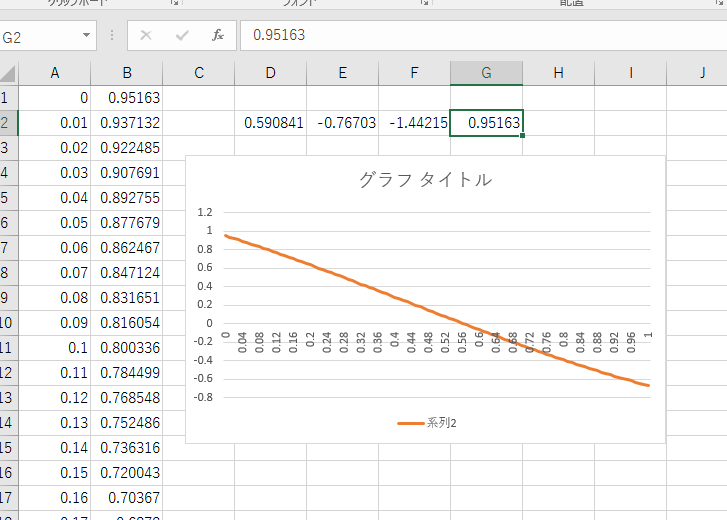
この辺は、まだ学習アルゴリズムのパラメータの調整など、どのようにすれば良いのか分かっていない。たかが3次元多項式のフィッティングでこれほどまでに計算量が必要とは思えないので、何かしら間違っているだけだと思うが...
ソースコード
import tensorflow as tf import numpy as np import random x_data = np.float32(np.random.rand(100)) # Random input y_data = np.sin(2*np.pi*x_data) + 0.3 * np.random.rand() # Construct a linear model. W3 = tf.Variable(random.random()) W2 = tf.Variable(random.random()) W1 = tf.Variable(random.random()) W0 = tf.Variable(random.random()) # y3 = W2*x_data*x_data + W1*x_data + W0 y4 = W3*x_data*x_data*x_data+W2*x_data*x_data + W1*x_data + W0 # Minimize the squared errors. loss = tf.reduce_mean(tf.square(y4 - y_data)) optimizer = tf.train.GradientDescentOptimizer(0.5) train = optimizer.minimize(loss) # For initializing the variables. init = tf.initialize_all_variables() # Launch the graph sess = tf.Session() sess.run(init) # Fit the plane. for step in xrange(0, 5000): sess.run(train) print step, sess.run(W3), sess.run(W2), sess.run(W1), sess.run(W0)