ゼロから作るDeep Learning ③ のDezeroをRubyで作り直してみる(ステップ33/ステップ34)

ゼロから作るDeep Learning ❸ ―フレームワーク編

ゼロから作るDeep Learning ③のDezero実装、勉強のためRubyでの再実装に挑戦している。計算グラフが表示できるようになって、いよいよ難しそうなところに突入していく。今回はステップ33とステップ34。

• ステップ33：ニュートン法を使った最適化を適用する。前回作成した高階微分の機能を使ってニュートン法を適用する。まずは2階微分を求める確認から。

begin
  x = Variable.new(np.array(2.0))
  y = f(x)
  y.backward()
  puts x.grad.to_s

  gx = x.grad
  x.cleargrad()
  gx.backward()
  puts x.grad.to_s
end

xを引数としてyを計算し、yからbackward()してx.gradに微分の結果を求める。この値をgxとして、gxをさらにbackward()して2階微分を求めるという作戦だ。

variable(24.0)
variable(44.0)

想定通りの計算を行うことができた。さらにニュートン法を適用する。

begin
  x = Variable.new(np.array(2.0))
  iters = 10

  for i in 0..iters do
    puts [i, x.to_s].to_s

    y = f(x)
    x.cleargrad()
    y.backward()

    gx = x.grad
    x.cleargrad()
    gx.backward()
    gx2 = x.grad

    x.data -= gx.data / gx2.data
  end
end

2階微分を用いて値をアップデートする。計算結果は以下の通りになった。問題なく計算できている。ニュートン法を実装できた！

[0, "variable(2.0)"]
[1, "variable(1.4545454545454546)"]
[2, "variable(1.1510467893775467)"]
[3, "variable(1.0253259289766978)"]
[4, "variable(1.0009084519430513)"]
[5, "variable(1.0000012353089454)"]
[6, "variable(1.000000000002289)"]
[7, "variable(1.0)"]
[8, "variable(1.0)"]
[9, "variable(1.0)"]
[10, "variable(1.0)"]

• ステップ34：sin関数の高階微分を求める。まずはsin関数とcos関数の定義から。

class Sin < Function
  def forward(x)
    np = Numpy
    y = np.sin(x)
    return y
  end
  def backward(gy)
    np = Numpy
    x = @inputs[0]
    gx = gy * cos(x)
    return gx
  end
end

def sin(x)
  return Sin.new().call(x)
end


class Cos < Function
  def forward(x)
    np = Numpy
    y = np.cos(x)
    return y
  end
  def backward(gy)
    np = Numpy
    x = @inputs[0]
    gx = gy * sin(x) * -1
    return gx
  end
end

def cos(x)
  return Cos.new().call(x)
end

これをベースにしてsin関数の高階微分を実現する。2階微分、3階微分、4階微分を求めてみる。matplotlibを使用するため、Numpyと同様にRubyのPycall機能を使用してmatplotlibをインポートする。

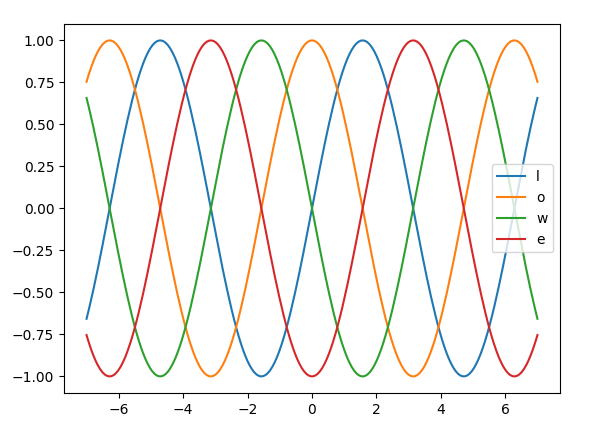
plt = PyCall.import_module('matplotlib.pyplot')

x = Variable.new(np.linspace(-7, 7, 200))
y = sin(x)
y.backward()

logs = [y.data.flatten()]

for i in 0..2 do
  logs.push(x.grad.data.flatten())
  gx = x.grad
  x.cleargrad()
  gx.backward()
end

labels = ["y=sin(x)", "y'", "y'", "y'''"]

logs.zip(labels).each{|log, l|
  plt.plot(x.data, log, label:l)
}
plt.legend(loc='lower right')
plt.show()

結果は以下のようになった。ラベルの表示が変だが、形になっているので今回は不問とする。上手く行っている。