Cpu0のバックエンドをLLVMに追加するプロジェクト、今回からは4章に入って、算術論理演算命令を追加する。まずは算術演算から。
算術演算において、特殊な演算ケースの場合は演算を最適化できる場合がある。この方式についても見ていく。
実装は以下。cpu0_chapter4ブランチに実装した。
以下の章を参考にした。
Arithmetic and Logic Instructions
Cpu0の算術演算を追加する。本章ではIRをGraphvizで表示する。DAGの変換のいくつかはGraphvizを使って説明する。算術演算命令を追加した後に、論理演算命令を追加する。
C言語のプログラムをコンパイルする中で、読者はC言語のプログラムがどのように変換されるのかについてみる。バックエンドの構造に加えて、読者はC言語の演算子がLLVM noIRにどのようにマッピングするのかについて説明する。本章ではHILOとC0レジスタクラスを追加する。読者は、汎用レジスタクラスだけでなく、このような特殊なレジスタの使用方法について学ぶ。
算術演算
+, -, *, <<, >> 演算子
+, -, *, SHL, SHLV(<<), SRA, SRAV, SHR, SHRV(>>)のための演算子が定義されている。
Chapter4_1では、C言語で言う +, -, *, <<, >> を扱うことができる。LLVM IRでadd, sub, mul, shl, ashrが定義されている。ashr命令(arithmetic shift right)命令は第1オペランドを符号拡張した形で右シフトする。
@@ -304,11 +405,36 @@ let Predicates = [DisableOverflow] in { def ADDu : ArithLogicR<0x11, "addu", add, IIAlu, CPURegs, 1>; } } +let Predicates = [Ch4_1] in { +let Predicates = [DisableOverflow] in { +def SUBu : ArithLogicR<0x12, "subu", sub, IIAlu, CPURegs>; +} +let Predicates = [EnableOverflow] in { +def ADD : ArithLogicR<0x13, "add", add, IIAlu, CPURegs, 1>; +def SUB : ArithLogicR<0x14, "sub", sub, IIAlu, CPURegs>; +} +def MUL : ArithLogicR<0x17, "mul", mul, IIImul, CPURegs, 1>; +} /// Shift Instructions +let Predicates = [Ch4_1] in { +// sra is IR node for ashr llvm IR instruction of .bc +def ROL : shift_rotate_imm32<0x1b, 0x01, "rol", rotl>; +def ROR : shift_rotate_imm32<0x1c, 0x01, "ror", rotr>; +def SRA : shift_rotate_imm32<0x1d, 0x00, "sra", sra>; +} let Predicates = [Ch3_5] in { def SHL : shift_rotate_imm32<0x1e, 0x00, "shl", shl>; } +let Predicates = [Ch4_1] in { +// srl is IR node for lshr llvm IR instruction of .bc +def SHR : shift_rotate_imm32<0x1f, 0x00, "shr", srl>; +def SRAV : shift_rotate_reg<0x20, 0x00, "srav", sra, CPURegs>; +def SHLV : shift_rotate_reg<0x21, 0x00, "shlv", shl, CPURegs>; +def SHRV : shift_rotate_reg<0x22, 0x00, "shrv", srl, CPURegs>; +def ROLV : shift_rotate_reg<0x23, 0x01, "rolv", rotl, CPURegs>; +def RORV : shift_rotate_reg<0x24, 0x01, "rorv", rotr, CPURegs>; +} def JR : JumpFR<0x3c, "jr", GPROut>;
例えば、shift_rotate_immは以下のように定義されている。srlなどの演算子はOpNodeに格納されれう。"shr"はstring instr_asmに格納されている。
class shift_rotate_imm<bits<8> op, bits<4> isRotate, string instr_asm,
SDNode OpNode, PatFrag PF, Operand ImmOpnd,
RegisterClass RC>:
FA<op, (outs GPROut:$ra), (ins RC:$rb, ImmOpnd:$shamt),
!strconcat(instr_asm, "\t$ra, $rb, $shamt"),
[(set GPROut:$ra, (OpNode RC:$rb, PF:$shamt))], IIAlu> {
let rc = 0;
}
- lshr: Logical SHift Right
- ashr: Arithmetic SHift right
- srl: Shift Right Logically
- sra: Shift Right Arithmetically
- shr: SHift Right
x >> 1は、x = x/2であると考えるとすると、演算子>>の実装ではlshrは符号付値では失敗する。同様にashrでは符号なし値で失敗する。したがって、符号付と符号なしの両方で演算を実行するためには、lshrとashrの両方が必要になる。
<<実装はlshrは"符号なしx = 1G"を満たすが、"符号付きx = 1G"では失敗することがわかる。 2Gは32ビット符号付き整数範囲(-2G〜2G-1)の外にあるので問題ない。 オーバーフローの場合、正しい結果をレジスタに保持する方法はない。 したがって、レジスタ内の値はすべて問題ない。 すべてのx << 1に対してlshrがx = x * 2を満たし、xの結果が範囲外でないことを確認できる。オペランドxが符号付きまたは符号なし整数であっても問題ない。
lbdex/input/ch4_math.ll
; Function Attrs: nounwind define i32 @_Z9test_mathv() #0 { %a = alloca i32, align 4 %b = alloca i32, align 4 %1 = load i32, i32* %a, align 4 %2 = load i32, i32* %b, align 4 %3 = add nsw i32 %1, %2 %4 = sub nsw i32 %1, %2 %5 = mul nsw i32 %1, %2 %6 = shl i32 %1, 2 %7 = ashr i32 %1, 2 %8 = lshr i32 %1, 30 %9 = shl i32 1, %2 %10 = ashr i32 128, %2 %11 = ashr i32 %1, %2 %12 = add nsw i32 %3, %4 %13 = add nsw i32 %12, %5 %14 = add nsw i32 %13, %6 %15 = add nsw i32 %14, %7 %16 = add nsw i32 %15, %8 %17 = add nsw i32 %16, %9 %18 = add nsw i32 %17, %10 %19 = add nsw i32 %18, %11 ret i32 %19 }
$ ./bin/llc -march=cpu0 -relocation-model=pic -filetype=asm ../lbdex/input/ch4_math.ll -o - .text .section .mdebug.abiO32 .previous .file "ch4_math.ll" .globl _Z9test_mathv # -- Begin function _Z9test_mathv .p2align 2 .type _Z9test_mathv,@function .ent _Z9test_mathv # @_Z9test_mathv _Z9test_mathv: .cfi_startproc .frame $sp,8,$lr .mask 0x00000000,0 .set noreorder .set nomacro # %bb.0: addiu $sp, $sp, -8 .cfi_def_cfa_offset 8 ld $2, 0($sp) ld $3, 4($sp) subu $4, $3, $2 addu $5, $3, $2 addu $4, $5, $4 mul $5, $3, $2 addu $4, $4, $5 shl $5, $3, 2 addu $4, $4, $5 sra $5, $3, 2 addu $4, $4, $5 addiu $5, $zero, 128 shrv $5, $5, $2 addiu $t9, $zero, 1 shlv $t9, $t9, $2 srav $2, $3, $2 shr $3, $3, 30 addu $3, $4, $3 addu $3, $3, $t9 addu $3, $3, $5 addu $2, $3, $2 addiu $sp, $sp, 8 ret $lr .set macro .set reorder .end _Z9test_mathv $func_end0: .size _Z9test_mathv, ($func_end0)-_Z9test_mathv .cfi_endproc # -- End function .section ".note.GNU-stack","",@progbits
オーバフローの検出を行う。
$ ./bin/clang -target mips-unknown-linux-gnu -c ch4_1_addsuboverflow.cpp -emit-llvm -o ch4_1_addsuboverflow.bc
$ llvm-dis ch4_1_addsuboverflow.bc -o -
%add = add nsw i32 %0, %1 %sub = sub nsw i32 %0, %1
-cpu0-enable-overflow=trueを追加した場合
$ ./bin/llc -march=cpu0 -relocation-model=pic -filetype=asm -cpu0-enable-overflow=true ch4_1_addsuboverflow.bc -o -
add $3, $3, $4
...
sub $3, $3, $4
-cpu0-enable-overflow=falseを追加した場合(デフォルト)
$ ./bin/llc -march=cpu0 -relocation-model=pic -filetype=asm -cpu0-enable-overflow=true ch4_1_addsuboverflow.bc -o -
addu $3, $3, $4
...
subu $3, $3, $4
現代のCPUでは、プログラマは加減算においてオーバフローを省略できる命令を利用することができる。しかし-cpu0-enable-overflow=trueを追加することにより、プログラマはオーバフロー例外を発生させることができる。通常、このオプションはデバッグ目的に利用する。
Graphvizでグラフを書き出す
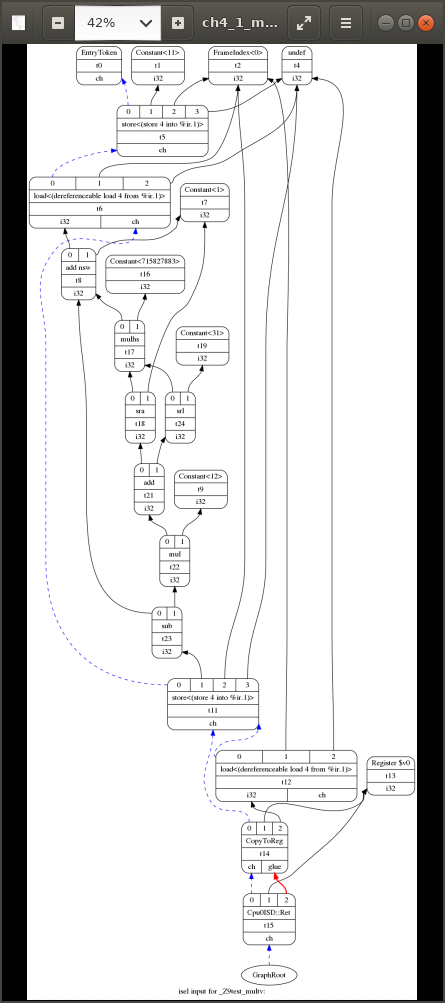
$ bin/clang -target mips-unknown-linux-gnu -c ../lbdex/input/ch4_1_mult.cpp -emit-llvm -o ch4_1_mult.bc $ bin/llc -view-dag-combine1-dags -march=cpu0 -relocation-model=pic -filetype=asm ./ch4_1_mult.bc -o ch4_1_mult.cpu0.s
%演算子と/演算子
%演算子はsrem IRに相当する。
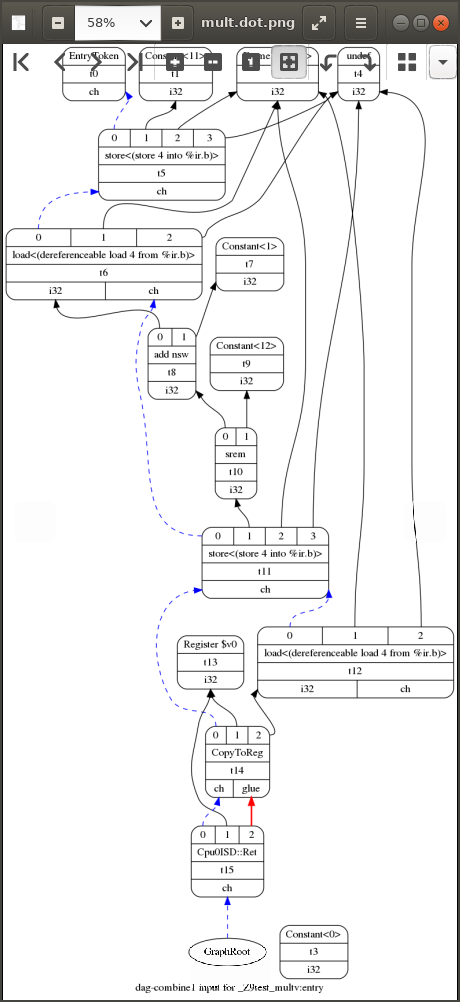
LLVMはsrem除算を乗算に変換し、DIVの演算コストを削減する。例えば、"int b = 11; b = (b+1)%12" はDAG上で図18のように最適化される。
この変換は少しややこしい。0xC x 0x2AAAAAAB = 0x2_00000004 となる(mulhs 0xC, 0x2AAAAAAAB) は、符号付乗算の上位32ビットを取得することを意味す。1ワードずつの数値の乗算結果は、通常、2ワード分の値を生成する(0x2, 0xAAAAAAAB)。この場合の上位の値、つまり0x2である。最終的な結果は(sub 12, 12)となり結果は0となる。これは(0x11+1)%12に相当する。
どうもこの0x2AAAAAABというのはマジック値であるらしい。%12で割り算をするためには、このような方法がとられるのか。
Armの解法
/// Multiply and Divide Instructions. def SMMUL : ArithLogicR<0x41, "smmul", mulhs, IIImul, CPURegs, 1>; def UMMUL : ArithLogicR<0x42, "ummul", mulhu, IIImul, CPURegs, 1>; //def MULT : Mult32<0x41, "mult", IIImul>; //def MULTu : Mult32<0x42, "multu", IIImul>;
SMMUL命令とUMMUL命令を使用して、乗算の結果から上位の32bitを取得することができる。
addiu $2, $zero, 12 smmul $3, $2, $3 shr $4, $3, 31
Mipsの解法
def mulhs : SDNode<"ISD::MULHS" , SDTIntBinOp, [SDNPCommutative]>; def mulhu : SDNode<"ISD::MULHU" , SDTIntBinOp, [SDNPCommutative]>;
MIPSの場合は、HILOレジスタに乗算命令の結果を格納するので、HIレジスタから値を持ってくればよい。
addiu $2, $zero, 12 mult $2, $3 mfhi $3 shr $4, $3, 31
%演算と/演算の完全サポート
上記の演算をより一般化して、"(b+1)%a"を計算する場合、LLVMはエラーを出してしまう。上記の剰余を乗算に変換する計算は、一般化したコードとして出力でき兄からだ。したがって、一般的には、上除算命令を実行した後にHILOレジスタから値を取ってくる方法が取られる。"c = a / b"は、"div a, b"と、"mflo c"の2つに分割される。
完全な"%"と"/"をサポートするためには、Chapter4_1のように以下を追加する。
- SDIV, UDIVを
Cpu0InstrInfo.tdに追加する。 copyPhysReg()を追加する。setOperationAction(ISD::SDIV, MVT::i32, Expand), ... setTargetDAGCombine(ISD::SDIVREM)と、PerformDivRemCombine()とPerformDAGCombine()を追加する。
static SDValue performDivRemCombine(SDNode *N, SelectionDAG& DAG, TargetLowering::DAGCombinerInfo &DCI, const Cpu0Subtarget &Subtarget) { ... // insert MFLO if (N->hasAnyUseOfValue(0)) { SDValue CopyFromLo = DAG.getCopyFromReg(InChain, DL, LO, Ty, InGlue); DAG.ReplaceAllUsesOfValueWith(SDValue(N, 0), CopyFromLo); InChain = CopyFromLo.getValue(1); InGlue = CopyFromLo.getValue(2); } ... return SDValue(); }
以下のコードを実行すると、div命令とmfhiが出力された。
lbdex/input/ch4_1_mult2.cpp
int test_mult() { int b = 11; int a = 12; b = (b+1)%a; return b; }
ld $2, 4($sp) addiu $2, $2, 1 ld $3, 0($sp) div $2, $3 mfhi $2 st $2, 4($sp)
ローテート命令
ローテート命令も同様に追加した。演算子自体は、以下で追加しているものと思われる。これで、Cのコードからローテートを推論できる。
/// Shift Instructions
let Predicates = [Ch4_1] in {
// sra is IR node for ashr llvm IR instruction of .bc
def ROL : shift_rotate_imm32<0x1b, 0x01, "rol", rotl>;
def ROR : shift_rotate_imm32<0x1c, 0x01, "ror", rotr>;
def SRA : shift_rotate_imm32<0x1d, 0x00, "sra", sra>;
}
論理演算子
&, |, ^, ! ==, !=, <, <=, >, >= 演算子をサポートする。以下のファイルに実装の追加を行う。
lib/Target/Cpu0/Cpu0ISelLowering.cpplib/Target/Cpu0/Cpu0InstrInfo.tdlib/Target/Cpu0/Cpu0Subtarget.h
-mcpu=cpu032Iと-mcpu=cpu032IIで生成されるプログラムが異なる。cpu032Iはcmp命令で処理、cpu032IIは比較命令で処理。cpu032Iとcpu032IIの命令セットの違いは、以下を確認。
Table 4 cpu032I Instruction Set https://jonathan2251.github.io/lbd/llvmstructure.html#id39
Table 5 cpu032II Instruction Set https://jonathan2251.github.io/lbd/llvmstructure.html#id40
cpu032I
ld $2, 28($sp)
ld $3, 24($sp)
cmp $sw, $2, $3
cpu032II
ld $2, 28($sp)
ld $3, 24($sp)
slt $2, $2, $3