前回は1量子ビットをC++でモデル化したのだが、それだけではほとんど何も表現出来ないので複数量子ビットに拡張したい。
複数量子ビットが表現できるようになれば、まずは例として加算器を動かしてみよう。 半加算器と全加算器が実現できればかなり面白い。
量子計算に大規模なコンピュータが必要な理由
最初は複数量子ビットを表現するのに量子ビットの数に線形比例するサイズの配列を用意すればよいのかと思っていたが、 考え方を完全に勘違いしていた。
そもそも量子ビットの表現にはの2種類が必要というところから始まる。
量子ビットが0であるということは
であり、一方で量子ビットが1であるということは
であるということを示している。
これはつまり量子ビットの1ビットを表現するために空間としては2通り必要と言う事である。
「0である場合」の量子ゲートの処理と「1である場合」の量子ゲートの処理が一度に表現できる。
つまり、上記の1量子ビットに対しての行列積を適用すると言う事は「量子の状態はわからないけれども、0にときはこっちの計算、1のときはこっちの計算を適用するよ」ということを同時に表現しているに等しい。
例えば、量子を向きを反転させるゲートだと$$\begin{pmatrix}
0 & 1 \\
1 & 0
\end{pmatrix}\begin{pmatrix}
\alpha \\
\beta
\end{pmatrix}$$ という行列を適用するが、量子ビット を
- 上側の要素は量子が0であることを示す。
- 下側の要素は量子が1であることを示す。
というようにデコードできるとする。
上記のゲートを適用すると となり、量子が0である確率と1である確率は反転する。
このように考えると、量子状態の表現では、量子ビットの数が増えるとその量子の状態を示す数だけ行列の大きさが増えると言う事がわかる。 つまり、
- 2量子ビットの場合 : 00, 01, 10, 11 の4状態 →行列のサイズは4
- 3量子ビットの場合 : 000, 001, 010, 011, 100, 101, 110, 111 の8状態 → 行列のサイズは8
となり、量子ビットの数がn_qbitsであるとすると、シミュレータ上で確保しなければならない行列のサイズはとなり指数関数的に増大する。
これが例えば50量子ビットになると
となり膨大な空間が必要なため、メモリを節約しつつコンピュータ上で計算する方法が必要不可欠となる訳だ。(といってもかなり疎行列なので圧縮する方法は沢山ありそうだが)
複数量子ビットをC++で表現しよう
量子ビットを表現する原理が少しわかってきたので、次にこれをどのようにプログラムで表現するか考えた。
基本的には、ビットの量子ビットを定義する場合、
長の配列を定義するのがよさそうだ。
配列の各要素には、量子がその状態をとる確率が入るという理解で良い気がする。
理解があいまいなのだが、複数量子ビットを表現する場合は行列の値にはどのような制限があるのだろうか?
1量子ビットだと、ブロッホ球上でという空間内に収まっている必要がある
(重ね合わせの状態だと
とか)。
これが複数量子ビットになるとどうなるんだ? 基本的にはブロッホ球が複数あるとして、それを1つの行列で表現したときにどのように制約を付け加えればよいのか良く分からない。
2018/09/30 追記。複数量子ビットの場合、長の配列の各要素を
と表現すると、制約は
となるらしい。
コメントで教えていただいた。ありがとうございます。
複数量子ビットを表現するためにQbitsクラスを定義した。
class Qbits { std::complex<double> *m_comp_amp; const size_t m_size;
コンストラクタでは量子ビットの初期値と、量子ビットのビット長を指定する。
Qbits (uint8_t val, const size_t size) : m_size(pow(2, size)) { m_comp_amp = new std::complex<double>[m_size]; for (size_t i = 0; i < size; i++) { m_comp_amp[i] = 0.0 + 0.0i; } m_comp_amp[val] = 1.0 + 0.0i; }
例えば3ビットの量子ビットを定義して、初期値が4である場合は配列の4番目が1.0で、それ以外は0.0とする。
複数量子ビットに採用する量子ゲートを作ろう
さて、複数量子ビットが定義できたのでさっそく何かしたい。 まずは半加算器を作る工程を考えて、必要なゲートを定義することにする。
半加算器は一般的に以下のような量子回路で定義されるらしい。
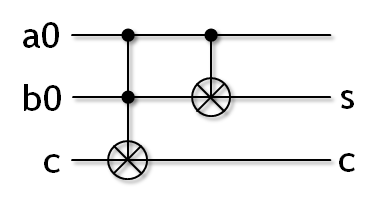
ここでCCNOTはトリフォゲートと呼ばれる。詳しくはWikipediaを参照のこと。 要するにある量子ビットを反転させるときに、その量子ビット以外の量子ビットがすべて1ならば反転し、そうでないときは反転しない。

一方でCNOTはこれの2ビット版である。2量子ビット(q1, q0)において、q1が1ならばq0が反転し、q1が0ならばq0は反転しない。
行列式では下記のように表現できるが、3ビット以上の量子ビットにも対応させたいことと、 反転するターゲットの量子ビットと残りの2量子ビットを指定する必要がある。
このため、CCNot()では3引数を取り、
とした。CNOTはその特殊版である(c0_idx == c1_idx)。
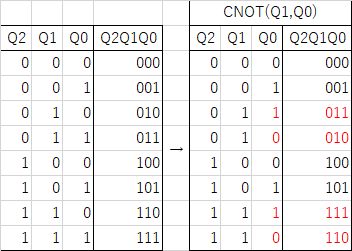

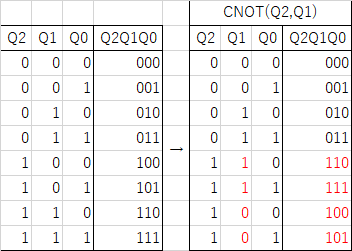
void CNot (int c_idx, int v_idx) { CCNot (c_idx, c_idx, v_idx); } void CCNot (int c0_idx, int c1_idx, int v_idx) { std::complex<double> *new_comp_amp = new std::complex<double>[m_size]; uint8_t c_bitmask = (1 << c0_idx) | (1 << c1_idx); uint8_t v_bitmask = 1 << v_idx; for (int idx = 0; idx < m_size; idx++) { int act_idx = idx; if ((idx & c_bitmask) == c_bitmask) { act_idx = idx ^ v_bitmask; } new_comp_amp[act_idx] = m_comp_amp[idx]; } for (int idx = 0; idx < m_size; idx++) { m_comp_amp[idx] = new_comp_amp[idx]; } }
たぶんもっと簡単に実装できると思う。プログラミング力が無い。。。 要するにbitmaskとなっているビットがすべて1であれば、ターゲットのビット位置を反転する。
勘違いしがちだが値を反転するのではなくて、配列の要素を入れ替える。
例えば、3ビットの量子ビットの[xyz]=[110]で、反転するターゲットの量子ビットをzとする。
判断を行うxyの2ビットが両方1なので、zは反転するのだが、あくまで8要素(3ビットの量子ビットなので)
[110](=6)と[111](=7)の要素を入れ替えるだけなのだ。
Wikipediaに乗っているの配列はまさにそれを示している。
量子ビットを使って半加算器を作ろう
というわけで、さっそく作ったCNot()とCCNot()を使って半加算器を構成した。
for (int val = 0; val < 4; val++) { Qbits qbits(val, 3); qbits.CCNot(1, 0, 2); // 量子ビット0,1の値によって、量子ビット2を反転させる qbits.CNot(0, 1); // 量子ビット0の値によって、量子ビット1を反転させる printf("qbit val = %d\n", qbits.Measure()); }
3量子ビットを定義した。
- ビット0 : 入力a
- ビット1 : 入力b, かつ計算後にはsum
- ビット2 : 計算後にcarryが入る
とする。入力を0から3まで変えて計算すると、それぞれ以下のようになった。
qbit val = 0 qbit val = 3 qbit val = 2 qbit val = 5
そっけない結果だが、
: sum=0, carry=0([000]->[000])
: sum=1, carry=0([001]->[011])
: sum=1, carry=0([010]->[010])
: sum=0, carry=1([011]->[101])
というビットが正しく表現できている。半加算器の完成だ。