Cirqの計算プロセスの続きである。Cirqがどのようにして量子状態の計算を行っているのかを見ていく。
とりあえず、前回から少しコードを変えた。アダマールゲートを使用するように変更する。アダマールゲートというのは、量子を重ね合わせの状態に持っていくゲートのことで、具体的には以下のような行列を計算する。
$$H=\dfrac{1}{\sqrt{2}}\begin{pmatrix} 1 & 1\\ 1 & -1 \end{pmatrix}$$
ただし、これはもう少し一般化できて、XZ軸の周りで回転させるときは下記のように表される(以下は https://www.appi.keio.ac.jp/Itoh_group/abe/pdf/ap2016_4.pdf より抜粋)。
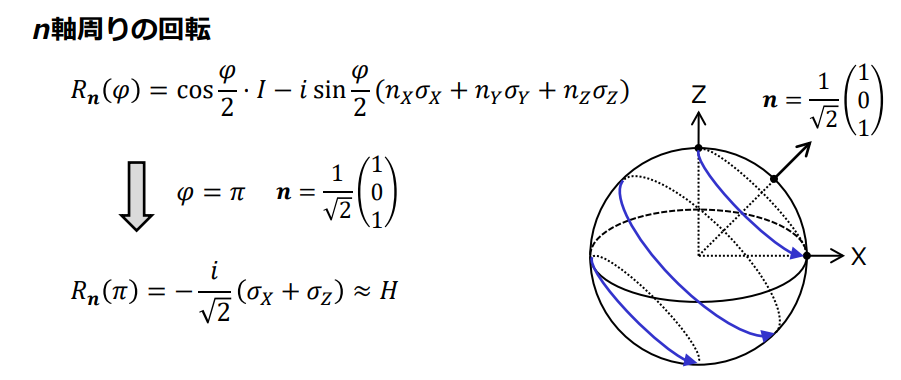
さて、下記のようにCirqで記述した量子回路はどのようにして計算されるのだろうか。
import cirq qbits = [cirq.GridQubit(0, i) for i in range(1)] circuit = cirq.Circuit() circuit.append(cirq.H.on(qbits[0])) simulator = cirq.google.XmonSimulator() results = simulator.run(circuit, repetitions=1000, qubit_order=qbits)
まずは回路の構成をprintを入れて見ていくと、以下のようになった。ExpWGateとExpZGateというもので構成されているようだ。そんな気がする。
(Pdb) c
> /home/msyksphinz/work/Cirq/cirq/google/sim/xmon_simulator.py(535)_simulator_iterator()
-> if isinstance(gate, xmon_gates.ExpZGate):
(Pdb) p circuit
cirq.Circuit(moments=[
cirq.Moment(operations=[
ExpWGate(half_turns=-0.5, axis_half_turns=0.5).on(cirq.GridQubit(0, 0)),
]),
cirq.Moment(operations=[
ExpZGate(half_turns=1.0).on(cirq.GridQubit(0, 0)),
]),
])
PDBなどでPythonのコードを追いかけていくと、実際のシミュレーションはcirq/google/sim/xmon_stepper.pyで実装されている。
ゲートを適用しているのは、以下のコードのようだ。
cirq/google/sim/xmon_stepper.py
class ThreadlessPool(object): """A Pool that does not use any processes or threads. Only supports map, close, and join, the later two being trivial. No enforcement of closing or joining is done, so map can be called repeatedly. """ # noinspection PyMethodMayBeStatic def map(self, func, iterable, chunksize=None): assert chunksize is None, 'Chunking not supported by SimplePool' return [func(x) for x in iterable]
それぞれfuncにはどのようなものが入っているのかを調査すると、以下のようになった。
func(x) = <function _w_within_shard at 0x7fbbbe0a62f0> func(x) = <function _norm_squared at 0x7fbbbe0a6510> func(x) = <function _renorm at 0x7fbbbe0a6598> func(x) = <function _clear_scratch at 0x7fbbbe0a6048> func(x) = <function _apply_scratch_as_phase at 0x7fbbbe0a6268> func(x) = <function _clear_scratch at 0x7fbbbe0a6048> func(x) = <function _single_qubit_accumulate_into_scratch at 0x7fbbbe0a60d0> func(x) = <function _apply_scratch_as_phase at 0x7fbbbe0a6268> func(x) = <function _clear_scratch at 0x7fbbbe0a6048> func(x) = <function _apply_scratch_as_phase at 0x7fbbbe0a6268> func(x) = <function _state_shard at 0x7fbbbe0a4c80>
例えば、Hゲートを実行しているのは_w_within_shardのような気がする。
- `cirq/google/sim/xmon_stepper.py``
def _w_within_shard(args: Dict[str, Any]): """Applies a W gate when the gate acts only within a shard.""" index = args['index'] half_turns = args['half_turns'] axis_half_turns = args['axis_half_turns'] state = _state_shard(args) pm_vect = _pm_vects(args)[index] num_shard_qubits = args['num_shard_qubits'] shard_size = 2 ** num_shard_qubits reshape_tuple = (2 ** (num_shard_qubits - 1 - index), 2, 2 ** index) perm_state = np.reshape( np.reshape(state, reshape_tuple)[:, ::-1, :], shard_size) cos = np.cos(-0.5 * np.pi * half_turns) sin = np.sin(-0.5 * np.pi * half_turns) cos_axis = np.cos(np.pi * axis_half_turns) sin_axis = np.sin(np.pi * axis_half_turns) new_state = cos * state + 1j * sin * perm_state * ( cos_axis - 1j * sin_axis * pm_vect) np.copyto(state, new_state)
各種関数にprintを挟んで実行してくと、以下のようになった。
func(x) = <function _w_within_shard at 0x7fbbbe0a62f0>
<perm_state = [0.+0.j 1.+0.j], pm_state = [ 1 -1]
< cos_axis - 1j * sin_axis * pm_vect = [6.123234e-17-1.j 6.123234e-17+1.j]>
<perm_state * (cos_axis - 1j * sin_axis * pm_vect) = [0.000000e+00+0.j 6.123234e-17+1.j]>
half_turns = -0.5, state = [1.+0.j 0.+0.j], new_state = [ 0.70710677+0.00000000e+00j -0.70710677+4.32978021e-17j]
func(x) = <function _norm_squared at 0x7fbbbe0a6510>
func(x) = <function _renorm at 0x7fbbbe0a6598>
state = [ 0.70710677+0.0000000e+00j -0.70710677+4.3297803e-17j]
new_state = [ 0.7071068+0.000000e+00j -0.7071068+4.329781e-17j]
func(x) = <function _clear_scratch at 0x7fbbbe0a6048>
func(x) = <function _apply_scratch_as_phase at 0x7fbbbe0a6268>
state = [ 0.7071068+0.000000e+00j -0.7071068+4.329781e-17j], _scratch_shard(args) = [0.+0.j 0.+0.j]
new_state = [ 0.7071068+0.000000e+00j -0.7071068+4.329781e-17j]
func(x) = <function _clear_scratch at 0x7fbbbe0a6048>
func(x) = <function _single_qubit_accumulate_into_scratch at 0x7fbbbe0a60d0>
func(x) = <function _apply_scratch_as_phase at 0x7fbbbe0a6268>
state = [ 0.7071068+0.000000e+00j -0.7071068+4.329781e-17j], _scratch_shard(args) = [-1.+0.j 1.+0.j]
new_state = [-3.090862e-08-0.7071068j 3.090862e-08-0.7071068j]
func(x) = <function _clear_scratch at 0x7fbbbe0a6048>
func(x) = <function _apply_scratch_as_phase at 0x7fbbbe0a6268>
state = [-3.090862e-08-0.7071068j 3.090862e-08-0.7071068j], _scratch_shard(args) = [0.+0.j 0.+0.j]
new_state = [-3.090862e-08-0.7071068j 3.090862e-08-0.7071068j]
func(x) = <function _state_shard at 0x7fbbbe0a4c80>
Counter({1: 502, 0: 498})
最初のアダマールゲートの適用で、[1.+0.j 0.+0.j]が[ 0.70710677+0.00000000e+00j -0.70710677+4.32978021e-17j] に変換されていることが分かる。
そのあとで_apply_scratch_as_phaseにより[ 0.7071068+0.000000e+00j -0.7071068+4.329781e-17j] から [-3.090862e-08-0.7071068j 3.090862e-08-0.7071068j] になっているが良く分からない。
つまりこのあたりを見ていけばCirqの量子計算の核の部分を見ることができそうだ。
ちなみに、Cirqはやはり量子ビットの数を大きくするとそのの行列を用意するようだ。
17ビットを超えるとそれ以上は
_within_shardは呼ばれなくなった。
- 量子ビット=1のとき。行列のサイズ=2
perm_state = [0.+0.j 1.+0.j] pm_vect = [ 1 -1] state = [1.+0.j 0.+0.j] new_state = [ 0.70710677+0.00000000e+00j -0.70710677+4.32978021e-17j]
- 量子ビット=2のとき。行列サイズ=4
perm_state = [0.+0.j 0.+0.j 1.+0.j 0.+0.j] pm_vect = [ 1 1 -1 -1] state = [1.+0.j 0.+0.j 0.+0.j 0.+0.j] new_state = [ 0.70710677+0.00000000e+00j 0. +0.00000000e+00j -0.70710677+4.32978021e-17j 0. +0.00000000e+00j]
- 量子ビット=5のとき。行列サイズ=32
perm_state = [0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 1.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j] pm_vect = [ 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1] state = [1.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j] new_state = [ 0.70710677+0.00000000e+00j 0. +0.00000000e+00j 0. +0.00000000e+00j 0. +0.00000000e+00j 0. +0.00000000e+00j 0. +0.00000000e+00j 0. +0.00000000e+00j 0. +0.00000000e+00j 0. +0.00000000e+00j 0. +0.00000000e+00j 0. +0.00000000e+00j 0. +0.00000000e+00j 0. +0.00000000e+00j 0. +0.00000000e+00j 0. +0.00000000e+00j 0. +0.00000000e+00j -0.70710677+4.32978021e-17j 0. +0.00000000e+00j 0. +0.00000000e+00j 0. +0.00000000e+00j 0. +0.00000000e+00j 0. +0.00000000e+00j 0. +0.00000000e+00j 0. +0.00000000e+00j 0. +0.00000000e+00j 0. +0.00000000e+00j 0. +0.00000000e+00j 0. +0.00000000e+00j 0. +0.00000000e+00j 0. +0.00000000e+00j 0. +0.00000000e+00j 0. +0.00000000e+00j]
ただし量子ビットを18ビットよりも大きくすると_w_within_shardは呼ばれなくなった。
別のアルゴリズムを使っているのだろうか。