次世代計算機講座に参加して、量子コンピュータについて俄然興味がわいてきた。
手っ取り早く量子コンピュータを試すためには、最近になっていろいろ手段が出てきている。
MicrosoftからはQ#、GoogleからはフレームワークとしてCirqがリリースされている。 これらの環境を使うのもいいけれども、あまり情報もないし折角なので自分で作ってみたい。
という訳で量子コンピュータシミュレータを1から自分で作るにはどうすればよいのか調べてみる。
参考にしたのは、次世代計算機講座で講演なされた京都大学の藤井啓祐先生の資料と、同じく藤井先生がCQ出版のInterfaceに寄稿された量子コンピュータのC言語モデルだ。 Interfaceに分かりやすい形で量子コンピュータのモデルが解説されているのは非常にありがたい。

Interface(インターフェース) 2018年 08 月号
- 出版社/メーカー: CQ出版
- 発売日: 2018/06/25
- メディア: 雑誌
- この商品を含むブログを見る
という訳で、まずはInterfaceの記事のコードをどんどんコピペしていく。
1量子ビットの表現
1量子ビットは複素数の変数としての組で表現されるので、複素型として2変数を用意する。
class Qbit { double _Complex m_comp_amp[2];
1量子ビットに対する操作
がどの程度傾いているかにより、0に近いか1に近いかが決まる。
そのランダム性は観測時に影響を与える。
ここでは、
0.0<= val <1.0 の乱数を生成して、その値との大小で最終的な0/1を決める。
int Measure () { double rand_val = rand() / static_cast<double>(RAND_MAX); double measure_val = pow(cabs(m_comp_amp[0]), 2); if (rand_val < pow(cabs(m_comp_amp[0]), 2)) { m_comp_amp[0] = 1; m_comp_amp[1] = 0; return 0; } else { m_comp_amp[0] = 0; m_comp_amp[1] = 1; return 1; } }
各種ゲートの適用
とりあえずは、アダマールゲートと回転ゲートを作ってみる。 アダマールゲートは以下のように表現される。
$$ \dfrac{1}{\sqrt{2}}\begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix} $$
次に、回転ゲートは以下のように表現される。
$$ \dfrac{1}{\sqrt{2}}\begin{pmatrix} 1 & 0 \\ 0 & e^{i\theta} \end{pmatrix} $$
というわけで、それぞれQbitクラスのメソッドとして以下のように表現した(というかかなりコピペした)。
void Hadamard () { m_comp_amp[0] = (m_comp_amp[0] + m_comp_amp[1]) / sqrt(2); m_comp_amp[1] = (m_comp_amp[0] - m_comp_amp[1]) / sqrt(2); } void Rotate (double theta) { m_comp_amp[0] = m_comp_amp[0]; m_comp_amp[1] = (cos(theta) + 1.0i * sin(theta)) * m_comp_amp[1]; }
回転ゲートの動作確認
という訳で、簡単な1量子ビットとそれに適用できるゲートは作ったので、藤井先生の例に出てくる1量子ビット演算を実行してみる。

ここで、回転ゲートの回転量をずつ細切れにして回転させて、1が出現する確率を測定する。
出現する確率は、1000回同様の量子計算を繰り返して測定する。つまり、以下のようになる。
for (int trial = 0; trial <= 10; trial++) { int count_one = 0; for (int count = 0; count < 1000; count++) { Qbit q_bit; q_bit.SetZero(); q_bit.Hadamard(); q_bit.Rotate(2 * M_PI * 0.1 * trial); q_bit.Hadamard(); if (q_bit.Measure() == 1) { count_one++; } } printf ("Trial = %d : count_one = %d\n", trial, count_one); }
上記のプログラムを実行すると、以下のようになった。
$ ./qbit_simulator Trial = 0 : count_one = 277 Trial = 1 : count_one = 340 Trial = 2 : count_one = 515 Trial = 3 : count_one = 737 Trial = 4 : count_one = 918 Trial = 5 : count_one = 982 Trial = 6 : count_one = 914 Trial = 7 : count_one = 748 Trial = 8 : count_one = 495 Trial = 9 : count_one = 331 Trial = 10 : count_one = 278
グラフを書くと、以下のようになった。
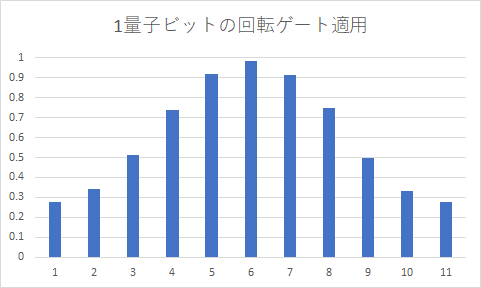
綺麗な三角関数が描けている。正しく計算できているようだ。
とりあえずはここまで。