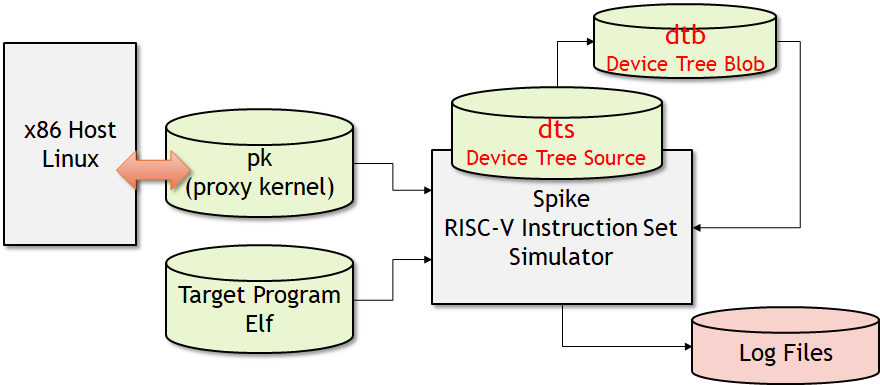
SiFiveをはじめとするRISC-Vの多くの実装では、プログラムの起動時にDevice Treeを読み取りに行くケースが多い。 事実として、RISC-Vの命令セットシミュレータであるSpike(riscv-isa-sim)は内部にDevice Treeが格納されており、ブートする前に読み取ることができる。 このDevice Treeによってブート時にどのような処理がなされているのか、解析してみることにした。
Spikeは実行時に以下のオプションを追加することでDevice Treeの情報を出力することができる。
$ spike --dump-dts [実行ファイル]
ちなみにこの実行ファイルは必要ないと思うのだが、今の仕様上必要なので入れておく。
/dts-v1/;
/ {
#address-cells = <2>;
#size-cells = <2>;
compatible = "ucbbar,spike-bare-dev";
model = "ucbbar,spike-bare";
cpus {
#address-cells = <1>;
#size-cells = <0>;
timebase-frequency = <10000000>;
CPU0: cpu@0 {
device_type = "cpu";
reg = <0>;
status = "okay";
compatible = "riscv";
riscv,isa = "rv64imafdc";
mmu-type = "riscv,sv48";
clock-frequency = <1000000000>;
CPU0_intc: interrupt-controller {
#interrupt-cells = <1>;
interrupt-controller;
compatible = "riscv,cpu-intc";
};
};
};
memory@80000000 {
device_type = "memory";
reg = <0x0 0x80000000 0x0 0x80000000>;
};
soc {
#address-cells = <2>;
#size-cells = <2>;
compatible = "ucbbar,spike-bare-soc", "simple-bus";
ranges;
clint@2000000 {
compatible = "riscv,clint0";
interrupts-extended = <&CPU0_intc 3 &CPU0_intc 7 >;
reg = <0x0 0x2000000 0x0 0xc0000>;
};
};
htif {
compatible = "ucb,htif0";
};
};
上記のDevice Tree情報はDevice Tree Compilerによりコンパイルされ、メモリ上に格納される。これをブート時に読み取るわけだ。
読み取るコードはriscv-pkから確認することができる。
riscv-pk/machine/minit.c
void init_first_hart(uintptr_t hartid, uintptr_t dtb) { // Confirm console as early as possible query_uart(dtb); query_htif(dtb); hart_init(); hls_init(0); // this might get called again from parse_config_string // Find the power button early as well so die() works query_finisher(dtb); query_mem(dtb); query_harts(dtb); query_clint(dtb); query_plic(dtb); wake_harts(); plic_init(); hart_plic_init(); //prci_test(); memory_init(); boot_loader(dtb); }
ここでは、dtsにも出てきているhtifの場所を解析するシーケンスについてみていく。query_htif()は以下のようになっている。
riscv-pk/machine/uart.c
void query_htif(uintptr_t fdt) { struct fdt_cb cb; struct htif_scan scan; memset(&cb, 0, sizeof(cb)); cb.open = htif_open; cb.prop = htif_prop; cb.done = htif_done; cb.extra = &scan; fdt_scan(fdt, &cb); }
ここでcbというのはコールバック関数のことだが
cb.open(): htifの情報を読み取るための下準備(初期化)cb.prop(): Propertyを読み取るコード(本体)cb.done(): htifの情報を読み終わった後の最終的な処理
に分けられている。cb.extraには、読み取った情報を格納しておくための領域として使用される。
fdt_scan()はDevice Tree BlobをParseするためのルーチンである。
これはDevice Treeのフォーマットに基づいてdtbをParseしていく。
そして、Propertyのツリーにたどり着くとcb.prop() (= htif_prop())を読み出してParseする。
(実際のParseについてはfdt_scan_helper()に実装があるが、ここでは本題ではないので割愛する)。
riscv-pk/machine/fdt.c
static uint32_t *fdt_scan_helper( uint32_t *lex, const char *strings, struct fdt_scan_node *node, const struct fdt_cb *cb) { struct fdt_scan_node child; struct fdt_scan_prop prop; int last = 0; ... case FDT_PROP: { assert (!last); ... lex += 3 + (prop.len+3)/4; cb->prop(&prop, cb->extra); break; }
htif_prop()で実行されているのは、Propertyの内容を確認して、HTIFのデバイス情報と合致すればHTIFは存在するという情報を掴むだけである。
riscv-pk/machine/htif.c
static void htif_prop(const struct fdt_scan_prop *prop, void *extra) { struct htif_scan *scan = (struct htif_scan *)extra; if (!strcmp(prop->name, "compatible") && !strcmp((const char*)prop->value, "ucb,htif0")) { scan->compat = 1; } }
全てのParseが終了すると、htif_done()が実行される。もし(上記のhtif_prop()により)HTIFに関するデバイス情報を発見していれば
グローバル変数のhtifに1が設定される。
これは実際のプログラム実行中にHTIFを使用できるか否かを確認するために使用される。
riscv-pk/machine/htif.c
static spinlock_t htif_lock = SPINLOCK_INIT; uintptr_t htif; ... static void htif_done(const struct fdt_scan_node *node, void *extra) { struct htif_scan *scan = (struct htif_scan *)extra; if (!scan->compat) return; htif = 1; }
ここで示したのはHTIFの簡単な例だが、それ以外の例えばUARTやメモリ領域の設定についても同様にDevice Treeの探索が実行され、アドレス情報などが設定用の変数に書き込まれて使用される。