GoogleのCirqのチュートリアルに記載されている、2Dの+/-イジングモデルの問題を解いてみる。

以下のようにエネルギー関数を定義して、Eを最小化できるような$s$を計算するのが問題だ。まずは、パラメータを固定して計算してみる。

$E(s _ {1},\dots,s _ {n}) = \sum _ {\lt i,j \gt} J _ {i,j}s _ i s _ j$

これは、以下の量子ビットで置き換えた式を最小化させる問題に等しい。

$H=\sum _ {\lt i,j \gt} J _ {i,j} Z _ i Z _ j + \sum _ i h _ i Z _ i$

これを自作量子コンピュータ・シミュレータで実装してみる。

波動関数の定義

量子ビットの定義

ここでは $3\times 3=9$ の量子ビットを定義した。

length = 3
qubits = [qbit.make_qbit() for i in range(length * length)]

これに対して、イジングモデルなので互いの量子ビットに対して関係性を記述することになる。

def rand2d(rows, cols):
    return [[random.choice([+1, -1]) for _ in range(rows)] for _ in range(cols)]

これにより、イジングモデルに対して以下のような力関係が生じることになった(これは乱数により変わる)。

transverse fields: [[1, -1, -1], [1, -1, 1], [-1, -1, -1]]
row j fields: [[1, 1, 1], [1, -1, 1]]
column j fields: [[1, -1], [-1, -1], [1, 1]]

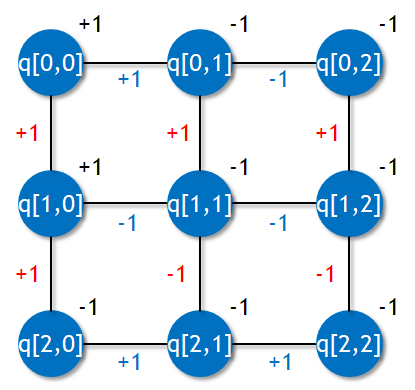
この状態で量子回路を組み立てていく。

def one_step(h, jr, jc, x_half_turns, h_half_turns, j_half_turns):
    length = len(h)
    rot_x_layer(length, x_half_turns)
    rot_z_layer(h, h_half_turns)
    rot_11_layer(jr, jc, j_half_turns)

それぞれの量子回路については以下の通りである。

def rot_x_layer(length, half_turns):
    """Yields X rotations by half_turns on a square grid of given length."""
    for i in range(length):
        for j in range(length):
            qbit.rotx(qubits[i * length + j], half_turns)

def rot_z_layer(h, half_turns):
    """Yields Z rotations by half_turns conditioned on the field h."""
    for i, h_row in enumerate(h):
        for j, h_ij in enumerate(h_row):
            if h_ij == 1:
                qbit.rotz(qubits[i * length + j], half_turns)

def rot_11_layer(jr, jc, half_turns):
    """Yeilds rotations about |11> conditioned on the jr and jc fields."""
    for i, jr_row in enumerate(jr):
        for j, jr_ij in enumerate(jr_row):
            if jr_ij == -1:
                qbit.x(qubits[(i + 0) * length + j])
                qbit.x(qubits[(i + 1) * length + j])
            yield qbit.rot11(qbits[(i + 0) * length + j],
                             qbits[(i + 1) * length + j])
            if jr_ij == -1:
                qbit.x(qubits[(i + 0) * length + j])
                qbit.x(qubits[(i + 1) * length + j])

    for i, jc_row in enumerate(jc):
        for j, jc_ij in enumerate(jc_row):
            if jc_ij == 1:
                yield qbit.rot11(qbits[(i * length) + (j + 0)],
                                 qbits[(i * length) + (j + 1)])

Rot11Gate

Cirqに実装されているRot11Gateについて、よく意味が分からない。マニュアルには以下のように書いてある。

cirq.Rot11Gate — Cirq 0.1 documentation

実装は良く分からないのだが、Rot11ということは2量子ビットが11の時に量子ゲートを回転させるらしい。 half_turns引数がついているので回転角も指定できる。とりあえずここでは実装を省略するために、2量子ビットが11の時にだけ量子の符号を反転させてみる。

void Qbits::Rot11 (int c0_idx, int c1_idx)
{
  std::complex<double> *new_comp_amp = new std::complex<double>[m_qbit_size];

  uint64_t c_bitmask = (1 << c0_idx) | (1 << c1_idx);
  for (size_t idx = 0; idx < m_qbit_size; idx++) {
    size_t act_idx = idx;
    if ((idx & c_bitmask) == c_bitmask) {
      new_comp_amp[act_idx] = -1.0 * m_comp_amp[idx];
    } else {
      new_comp_amp[act_idx] = m_comp_amp[idx];
    }
  }
  for (size_t idx = 0; idx < m_qbit_size; idx++) {
    m_comp_amp[idx] = new_comp_amp[idx];
  }
}

エネルギー関数を定義

量子回路を組んだら、それを測定して、エネルギー関数を適用する。

Cirqのチュートリアルにエネルギー関数が定義されているので、それをそのまま活用させてもらう。

one_step(h, jr, jc, 0.1, 0.2, 0.3)

def energy_func(length, h, jr, jc):
    def energy(measurements):
        meas_list_of_lists = [measurements[i:i + length] for i in range(length)]
        pm_meas = 1 - 2 * np.array(meas_list_of_lists).astype(np.int32)
        tot_energy = np.sum(pm_meas * h)
        for i, jr_row in enumerate(jr):
            for j, jr_ij in enumerate(jr_row):
                tot_energy += jr_ij * pm_meas[i, j] * pm_meas[i + 1, j]
        for i, jc_row in enumerate(jc):
            for j, jc_ij in enumerate(jc_row):
                tot_energy += jc_ij * pm_meas[i, j] * pm_meas[i, j + 1]
        return tot_energy
    return energy

def obj_func(hist):
    return np.sum(k * v for k,v in hist.items()) / 1000

energy_hist = collections.Counter()
func = energy_func(3, h, jr, jc)

for i in range(0, 1000):
    bits = [0 for i in range(length * length)]
    val = 0
    for idx in range(length * length):
        bits[idx] = qbit.val(qubits[idx])
        val = (val << 1) | bits[idx]
    val = func(bits)
    energy_hist[val] += 1