ヘネパタ第6版こと、"Computer Architecture 6th Edition" では、第7章でドメイン固有アーキテクチャの章が新設された。これを機会に、しっかり読んでいこう。

Computer Architecture, Sixth Edition: A Quantitative Approach (The Morgan Kaufmann Series in Computer Architecture and Design)

作者: John L. Hennessy,David A. Patterson
出版社/メーカー: Morgan Kaufmann
発売日: 2017/12/07
メディア: ペーパーバック
この商品を含むブログを見る

7.3章はがっつりディープニューラルネットワークの内容だ。今回は多層パーセプトロン、畳み込みニューラルネットワーク、再帰型ニューラルネットワーク。

これは著者が読んだ内容をまとめているだけなので、誤訳、理解不足により誤っている可能性があります！鵜呑みにしないようにお願いします。 2018/01/03 追記。フューチャーマップ(future map)→特徴マップ(feature map)の誤訳でした。訂正します。

多層パーセプトロン

MLPはDNNの原型である。それぞれ新しいレイヤは非線形関数Fの集合であり、ひとつ前のレイヤの全ての出力と重みを掛け合わせた値 $y_n=F(W\times y_{n-1})$ で構成されている。重み付き加算値は、出力値と重みのベクトル-行列積で構成されている(図7.7を参照のこと)。このようなレイヤは"Fully-Connected"と呼ばれており、これは各出力ニューロンの結果は、前のレイヤの入力ニューロンに依存しているからである。

DNNの形によって、レイヤ当たりのニューロン量、演算量、重みの量は計算することが出来る。最も簡単なのはMLPで、入力ベクトルと重み行列のベクトル-行列積を実行するだけである。以下に、推論に必要な重みの数と演算量のパラメータと式を示す(ここでは、積和演算については2演算として計算している)。

$\text{Dim}[i$ ]: 出力ベクタの次元数。ニューロンの数と同様である。
$\text{Dim}[i-1$ ]: 入力ベクタの次元数
重みの数: $\text{Dim}[i-1]\times \text{Dim}[i$ ]
演算量: $2\times\text{重みの数}$
演算量/重み: 2

最後の項は「演算強度(operational intensity)」と呼ばれ、第4章でルーフラインモデルとして議論したものである。私たちは、通常、チップに収まらない何百万という重みが存在する可能性があるため、重みあたりの演算量という指標を用いる。例えば、1ステージ当たりでMLPの次元数は7.9章で $\text{Dim}[i-1]=4096, \text{Dim}[i]=2048$ であり、したがってニューロンの数は2048個、そして重みの数は8,388,608であり、演算量は16,777,216であり、演算強度は2である。ルーフラインモデルで述べたように、演算強度が低い場合は、高い演算性能を出すのが難しくなる。

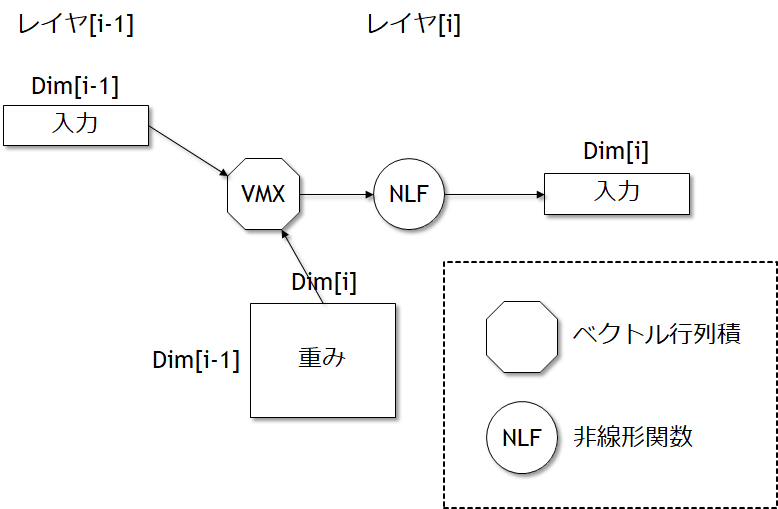
図7.7 MLPは左側の入力レイヤ[i-1]からのデータを受け取り右側のレイヤ[i]に出力する。

ReLUはMLPでは有名な非線形関数である。多くの場合は入力レイヤと出力レイヤの次元数は異なる。このようなレイヤはfully connectedレイヤと呼ばれ、これは出力レイヤは前のレイヤのすべての入力に依存しているからである。これは殆どの値がゼロでも同じことがいえる。ある研究では、前のレイヤの値の44%がゼロであるが、これはReLUにより負の数がすべてゼロにされるからであると推定することが出来る。

畳み込みニューラルネットワーク

CNNはコンピュータビジョンのアプリケーションにおいて広く利用されている。画像は2次元の構造をしており、隣接するピクセルは関係性を見出しやすい。CNNは前のレイヤからの出力値のうち、空間的に隣接する領域の情報を非線形関数を受け取り、何度も再利用している重みを掛け合わせる。

CNNのアイデアの背景には、各レイヤは画像の抽象レベルに対応していると考えることが出来る。例えば、最初のレイヤは水平方向と垂直方向のラインを特定するためのレイヤと考えることが出来る。 2番目のレイヤは、コーナーを検出するためにこれらの情報を組み合わせるためのレイヤである。次のステップでは四角形と丸を識別するためのレイヤである。次のレイヤは犬の部品、例えば目屋耳などを識別するためのレイヤである。より高いレイヤでは、犬の種類名の違いなどの特徴を識別するためのレイヤである。

各ニューラルレイヤは2次元の「特徴マップ(feature map)」と呼ばれる、特徴マップの各セルが入力画像の対応する領域化から1つの特徴を識別するための情報を生成する。

図7.8は入力画像から2×2のステンシル計算を行い、最初の特徴マップの要素を生成するための最初のポイントを示している。「ステンシル計算(stencil computation)」は固定のパタンから、隣接するセルを使って、アレイ中のすべてのエレメントを更新する。出力された特徴マップの数はあなたが画像から何個の異なる特徴を抽出するかと、ステンシルを抽出するために利用するストライドの量に依存する。

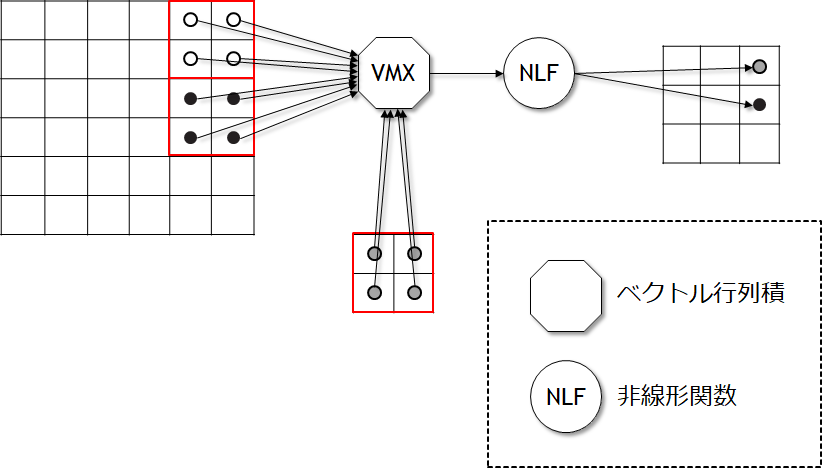
図7.8 CNNの最初のステップの簡単な図。この例では、入力画像の4つのピクセルのすべてのグループは同じ4つの重みと掛け合わされ、出力セルの特徴マップを生成する。この図では入力ピクセルを2ストライドずつグループにしているが、他の可能性もありうる。MLPと比較するためには、2×2の畳み込みを小さなfully connectedな演算として1出力を生成するものと考えることが出来る。図7.9では特徴マップを3次元のベクトルに変換する方法について示している。

通常、画像は単一のものでは無く、フラットな2次元のレイヤであるため、この処理はより複雑なものになる。典型的には、画像データは赤、青、黄色の3レベルの情報を持っている。例えば、2×2のステンシルは12個の要素にアクセスすることになる: 2×2の赤ピクセル、2×2の青ピクセル、2×2の緑ピクセルである。この場合には、2×2のステンシルで3レベルの3つの竜力レベルの画像では、出力特徴マップ当たり12個の重みが必要である。

図7.9は入力と、最初のレイヤから生成された出力特徴マップの任意数について示している(xxx)。計算は1組の重みを有するすべての入力特徴マップに対する3次元ステンシルであり、1つの出力特徴マップを生成する。

数学が好きな読者のために説明すると、もし入力特徴マップと出力特徴マップが同一で1であり、ストライドが1である場合、2次元CNNの単一レイヤは2次元の離散した畳み込みである。

図7.9に見るように、CNNはMLPよりも複雑である。重みと演算量についてパラメータと等式を示す。

$\text{DimFM}[i-1]$ : (正方形の)入力特徴マップの次元数
$\text{DimFM}[i]$ : (正方形の)出力特徴マップの次元数
$\text{DimSten}[i]$ : (正方形の)ステンシルの次元数
$\text{NumFM}[i-1]$ : 特徴マップ入力の数
$\text{NumFM}[i]$ : 特徴マップの出力の数
ニューロンの数 : $\text{NumFM}[i]\times\text{DimFM}[i]^2$
出力特徴マップあたりの重みの数 : $\text{NumFM}[i-1]\times\text{DimSten}[i]^2$
レイヤ当たりの重みの数 : $\text{NumFM}[i]\times\text{出力特徴マップあたりの重みの数}$
特徴マップあたりの演算量 : $2\times\text{DimFM}[i]^2\times\text{出力特徴マップあたりの重みの数}$
レイヤあたりの演算量 : $\text{NumFM}[i]\times\text{出力特徴マップあたりの演算量}$ = $2\times\text{DimFM}[i]^2\times\text{NumFM}[i]\times\text{出力特徴マップあたりの重みの数}$ = $2\times\text{DimFM}[i]^2\times\text{DimFM}[i]^2\times\text{レイヤ当たりの重みの数}$
演算量/重み : $2\times\text{DimFM}[i]^2$

7.9章のCNNは、 $\text{DimFM}[i-1]=28, \text{DimFM}[i]=14$ , $\text{DimSten}[i]=3$ , $\text{NumFM}[i-1]=64(入力特徴マップの数)$ , $\text{NumFM}[i]=128(出力特徴マップの数)$ である。このレイヤでは25,088個のニューロン、73,728個の重み、28,901,376演算量が必要である。したがって演算強度は392である。私たちの例では、CNNはMLPのfully connectedなレイヤよりも重みの量は少なく、高い演算強度を持っている。

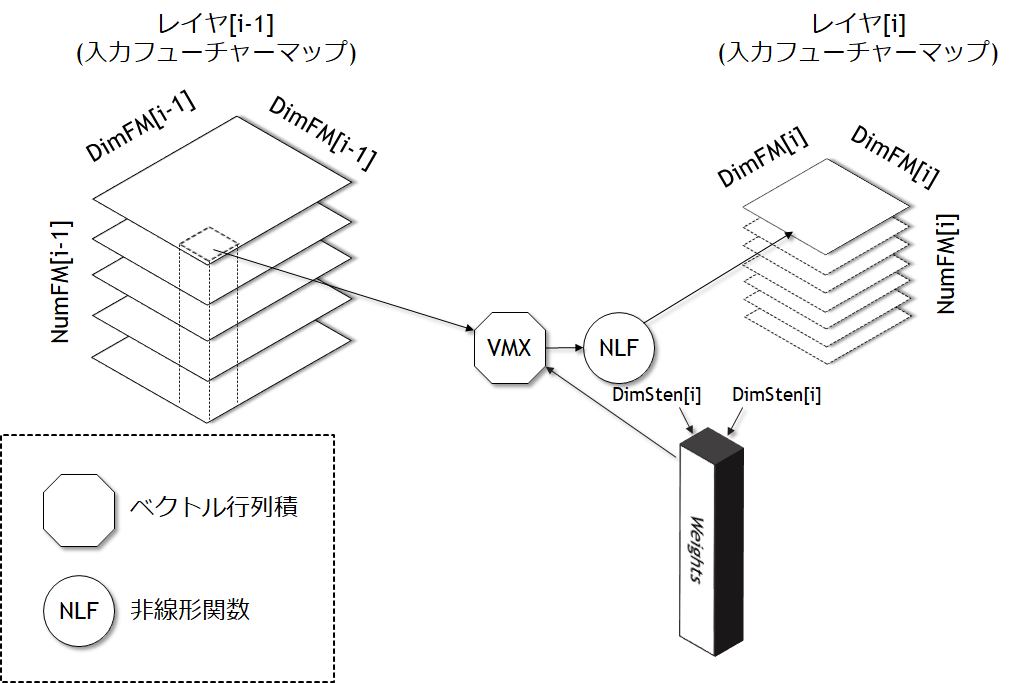
図7.9 CNNのレイヤ[i-1]における入力特徴マップ(左側)からレイヤ[i]の出力特徴マップへの一般的なステップ。

3次元の入力特徴マップから、単一の出力特徴マップへの生成を行う。各出力特徴ーマップはそれぞれ独立した重みの集合を持っており、ベクトル―行列積によりすべての要素が演算される。点線は将来衛星される特徴マップである。この図が示しているように、入力および出力特徴マップの次元及び数はしばしば異なるものになる。MLPと同様に、ReLUはCNNのための有名な非線形関数である。

再帰型ニューラルネットワーク

3番目のDNNの型はRNNである。これは音声認識や言語翻訳などの分野で有名なネットワークである。 RNNはDNNモデルに対してステートを追加して順次入力を追加することにより、RNNが事実を記録することが出来るようになる。これはハードウェアにおける組み合わせ論理とステートマシンの違いと似ている。例えば、あなたが非との性別を学習したい場合、翻訳した言葉を記憶しておき、あとでもう一度パスさせたいということもあるであろう。 RNNの各レイヤは前のレイヤで生成した重みと入力の掛け合わしたものと、前の状態を入力として受け取る。重みは、時間のステップで再利用される。

「Long short-term memory(LSTM)」はRNNの種類としては現在断然有名なネットワークである。 LSTMはこれまでのRNNが重要な長期情報を記憶することが出来なかった問題に解決策を示した。

これまでの2つのDNNと異なり、LSTMは仮想的なデザインである。 LSTMは「セル(cell)」と呼ばれるモジュールから構成されている。セルは完全なDNNモデルを生成するためのテンプレートもしくはモデルと考えることが出来る。これはMLPを並べて完全なDNNモデルを生成させる問題と似ている。

図7.10はLSTMセルがどのようにお互いにリンクしているのかを示している。各セルは左から右に接続されており、ひとつのセルの出力が次のセルの入力へ接続されている。またこれは図7.10においてトップダウンで時間軸として展開されている。したがって、文章はアンロールされたループの1回の繰り返し当たりの入力となる。 LTSMの名前が示す通りの長期記憶と短期記憶の情報は、トップダウンであるイタレーションから次のイタレーションへ渡される。

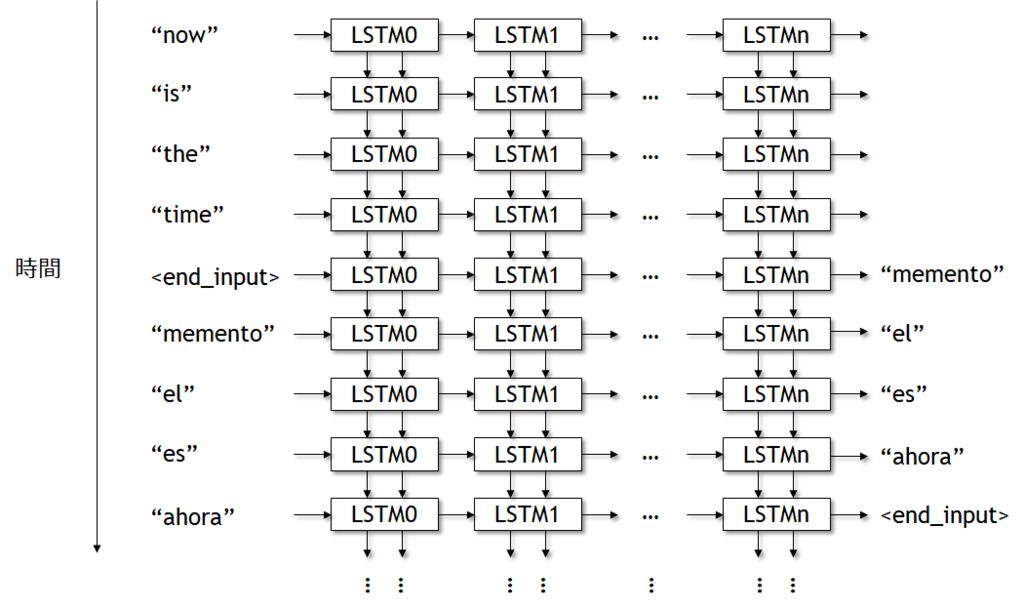
図7.10 互いに接続されたLSTMセル

図7.11にLSTMセルの内容を示す。図7.10に示したように、入力値は左側、出力値は右側に示しており、2つのメモリの入力は上側、2つのメモリの出力は下側に示している。

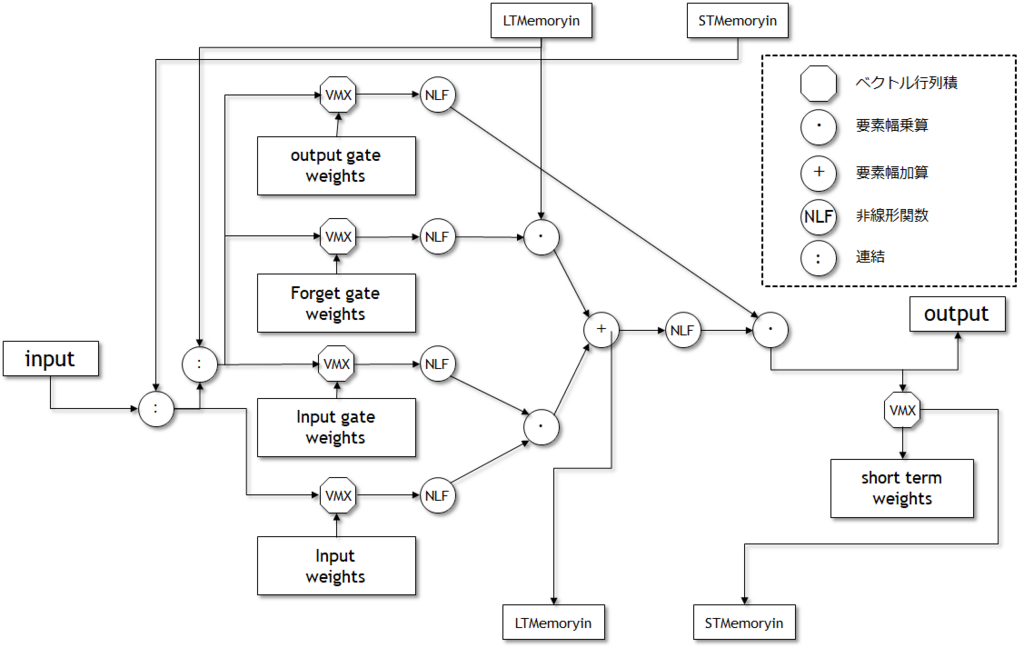
図7.11 LSTMセルは5つのベクトル行列積、3つの要素幅乗算、1つの要素幅加算、6つの非線形関数を含んでいる。

各セルには5つのベクトル行列積を実行し、5つの独立した重み値を使っている。入力値の行列積は図7.7のMLPのようになっている。 3つのそれ以外の行列積は「ゲート(gates)」と呼ばれており、あるソースから標準出力もしくはメモリ出力として渡される際の情報をゲートもしくは制限するためのものである。ゲートあたりに通過する情報はこれらの重みにより設定される。もし重みがほとんどゼロ、もしくは小さな値であった場合、多くの情報は通過しない; 一方で、これらの重みがほとんどが大きければ、ゲートはほとんどの情報を通過させる。 3つのゲートは「入力ゲート(input gate)」「出力ゲート(output gate)」「忘却ゲート(forget gate)」と呼ばれている。最初の2つのゲートは入力と出力をフィルタリングし、最後のゲートはLong-termメモリパス中で何を忘却するかを決定する。

Short-termメモリの出力はShort-Termの重みとベクトル行列積を通じて、そのセルの出力となる。 SHort-termラベルはセルの入力を直接使用されないため適用される (xxx)。

LTSMセルの入力と出力はすべて互いに接続されているため、3つの入力・出力のペアのサイズは同一である。セルの中身を見てみると、すべての入力と出力はしばしば同じサイズであるという十分な依存が存在する。これらはすべて同じサイズ出ると仮定し、これを $text{Dim}$ とする。

たとえそうであっても、ベクトル―行列積はすべて同じサイズではない。 3つのゲートの乗算は $3\times\text{Dim}$ である。なぜならば、LSTMはすべての3つの入力を接続するからである。入力のベクトルは $2\times\text{Dim}$ である。なぜならばLSTMは入力とShort-termメモリの入力を1つのベクトルとして接続するからである。最後の乗算の入力は単純に出力に接続されるため $1\times\text{Dim}$ である。

したがって、重みと演算量は以下のように計算できる。

セル当たりの重みの数 : $3 \times(3\times\text{Dim}\text{Dim})+(2\times\text{Dim}\times\text{Dim})+(1\times\text{Dim}\text{Dim})=12\times\text{Dim}^2$
1セルあたりの5つのベクトル行列乗算量: $2\times\text{セル当たりの重みの数}$
3要素の乗算及び1回の加算に演算量(ベクトルはすべて出力のサイズ): $4\times\text{Dim}$
セル当たりの演算量(5ベクトル行列積と4要素幅の演算): $24\times\text{Dim}^2+4\times\text{Dim}$
演算量/重み: ～2