CNTK 2.0について勉強する。CNTKはTensorFlowと同様にチュートリアルが用意されており、これを進めていくことにしよう。
まずは、Logistic Regression(回帰分析)をCNTKのニューラルネットワークで構成し、回帰分析を学習してみる。
https://github.com/Microsoft/CNTK/blob/v2.0/Tutorials/CNTK_101_LogisticRegression.ipynb
CNTK 2.0を用いた回帰分析
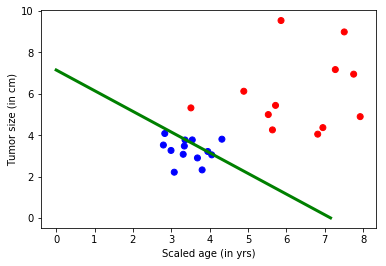
CNTK 101チュートリアルでは、回帰分析を用いてデータの分類を行う。ここで例として取り上げられているのは、2種類の要素(年齢、腫瘍の大きさ)に対するガン腫瘍であるかどうかを識別する回帰分析だ。つまり、X軸を年齢、Y軸を腫瘍の大きさ都市、それがガン腫瘍であるかどうかを識別するものとなる。 以下のようなグラフをプロットすることができ、青色のプロットが良性腫瘍、赤色のプロットが悪性腫瘍となる。 さらに、下記のような回帰直線を引くことで、良性と悪性の境界線を引くことができるようになる。
from IPython.display import Image Image(url="https://www.cntk.ai/jup/cancer_data_plot.jpg", width=400, height=400)

Image(url= "https://www.cntk.ai/jup/cancer_classify_plot.jpg", width=400, height=400)

回帰分析においては、各種パラメータをニューラルネットワークに入力し、良性か悪成果を示すラベル(0, 1)を出力するということになる。これにはSigmoid関数とSoftmax関数を利用する。
まず、Python実行環境について確認しておこう。CNTKでは環境変数を利用して実行する環境を選択する(GPU or CPU)。デフォルトでは、CNTKは選択可能なデバイスの中で最良のもの(CPUよりGPU)を選択する。
まあ、下記の試行では私の環境ではCPUもGPUも特に選択されなかったのだけど。なんでだ。
# Import the relevant components from __future__ import print_function import numpy as np import sys import os from cntk import * import cntk as C # Select the right target device when this notebook is being tested: if 'TEST_DEVICE' in os.environ: if os.environ['TEST_DEVICE'] == 'cpu': C.device.try_set_default_device(C.device.cpu()) print ("CNTK selected CPU device") else: C.device.try_set_default_device(C.device.gpu(0)) print ("CNTK selected GPU device")
まずは入力データの生成を行う。ここでは2次元のデータとして、X軸は年齢、Y軸は腫瘍の大きさを示すデータを生成する。
# Define the network input_dim = 2 num_output_classes = 2 # Ensure we always get the same amount of randomness np.random.seed(0) # Helper function to generate a random data sample def generate_random_data_sample(sample_size, feature_dim, num_classes): # Create synthetic data using NumPy. Y = np.random.randint(size=(sample_size, 1), low=0, high=num_classes) # Make sure that the data is separable X = (np.random.randn(sample_size, feature_dim)+3) * (Y+1) # Specify the data type to match the input variable used later in the tutorial # (default type is double) X = X.astype(np.float32) # converting class 0 into the vector "1 0 0", # class 1 into vector "0 1 0", ... class_ind = [Y==class_number for class_number in range(num_classes)] Y = np.asarray(np.hstack(class_ind), dtype=np.float32) return X, Y # Create the input variables denoting the features and the label data. Note: the input # does not need additional info on number of observations (Samples) since CNTK creates only # the network topology first mysamplesize = 32 features, labels = generate_random_data_sample(mysamplesize, input_dim, num_output_classes)
いくつか主要なコードをまとめておこう。このデータ群はかなり恣意的に作られている。つまり、最初のYの生成時にあらかじめ両性候補、悪性候補を01で区分けしておき、良性のものは小さな倍率、悪性のものは大きな倍率で配列Xを生成することでデータに恣意的な偏りを発生させている。 ニューラルネットワークでその偏りを認識して、境界線を引こうという考え方だ。
また、class_ind変数んについても、Y値(良性か悪性かを示す)によってYの値を決めておき、最終的にfeaturesとlabelsは以下のように生成されているはずだ。
同様にプロットしてみると以下のようになる。
print (np.hstack((features, labels))) # Plot the data import matplotlib.pyplot as plt %matplotlib inline # given this is a 2 class () colors = ['r' if l == 0 else 'b' for l in labels[:,0]] plt.scatter(features[:,0], features[:,1], c=colors) plt.xlabel("Scaled age (in yrs)") plt.ylabel("Tumor size (in cm)") plt.show()
[[ 3.44386315 3.33367443 1. 0. ]
[ 8.98815823 5.58968353 0. 1. ]
[ 6.62613535 4.29180861 0. 1. ]
[ 0.44701019 3.65361857 1. 0. ]
[ 7.7288723 4.51566982 0. 1. ]
[ 10.53950882 3.09126854 0. 1. ]
[ 6.09151697 5.62563229 0. 1. ]
[ 9.06555843 8.93871784 0. 1. ]
[ 6.30989504 6.75632524 0. 1. ]
[ 4.22442865 2.03840709 0. 1. ]
[ 5.30417585 6.31269789 0. 1. ]
[ 4.23029089 4.2023797 1. 0. ]
[ 2.61267328 2.69769716 1. 0. ]
[ 3.90289402 3.15996408 0. 1. ]
[ 1.29372978 4.95077562 1. 0. ]
[ 2.49034786 2.56192565 1. 0. ]
[ 1.74720466 3.77749038 1. 0. ]
[ 1.3861022 2.78725982 1. 0. ]
[ 2.10453343 3.38690257 1. 0. ]
[ 4.97838974 3.63873553 0. 1. ]
[ 2.97181773 3.42833185 1. 0. ]
[ 6.13303423 6.60494375 0. 1. ]
[ 4.73135567 5.27451754 0. 1. ]
[ 2.32753944 2.6404469 1. 0. ]
[ 2.18685365 1.2737174 1. 0. ]
[ 6.3548522 5.19643831 0. 1. ]
[ 2.73960328 6.92556429 0. 1. ]
[ 4.18540335 6.1038909 0. 1. ]
[ 7.4581809 6.25796604 0. 1. ]
[ 4.13940048 1.76517415 1. 0. ]
[ 6.80468321 4.63037968 0. 1. ]
[ 2.12920284 2.42115045 1. 0. ]]
[f:id:msyksphinz:20170618215531p:plain]
ネットワークモデルの作成
ここでは、回帰分析のネットワークを作成する。入力値x_iに対して重みw_iの積を計算し、さらにバイアス値を加算する。
CNTKでは、入力値の定義として以下のinput_variableを利用する。
- input variable: ユーザコードの入力値を受け取るためのコンテナ。inputの形は入力されるデータの形と同一である。例えば、入力が高さ10ピクセル、幅5ピクセルのデータであれば、入力値の次元は2となる。
feature = C.input_variable(input_dim, np.float32)
ネットワークをセットアップする。ここではlinear_layerという関数を作成する。ここでは、入力値であるxと重みwの積を計算し、bias_paramを加算する。timesは行列積を実行するCNTKの組み込み関数である。weight_param変数は(2, 2)の行列、bias_param変数は(1, 2)の行列なので、結果は(1, 2)の行列積となる。
# Define a dictionary to store the model parameters mydict = {"w":None,"b":None} def linear_layer(input_var, output_dim): input_dim = input_var.shape[0] weight_param = C.parameter(shape=(input_dim, output_dim)) bias_param = C.parameter(shape=(output_dim)) mydict['w'], mydict['b'] = weight_param, bias_param return C.times(input_var, weight_param) + bias_param output_dim = num_output_classes z = linear_layer(feature, output_dim)
最後に出力値に対して、Softmax関数を適用して終了となる。さらに、誤差を計算するためにeval_errorを定義する。
classification_error(output_vector, target_vector): 類似度を計算する。output_vectorの最大値が、target_vectorと一致しているかをチェックする。
print (C.classification_error([[1., 2., 3., 4.]], [[0., 0., 0., 1.]]).eval()) print (C.classification_error([[1., 2., 3., 4.]], [[0., 0., 1., 0.]]).eval()) print (C.classification_error([[1., 2., 3., 4.]], [[5., 0., 1., 0.]]).eval()) label = C.input_variable((num_output_classes), np.float32) loss = C.cross_entropy_with_softmax(z, label) eval_error = C.classification_error(z, label)
[[ 0.]]
[[ 1.]]
[[ 1.]]
トレーニングの構成
誤差を最小にするための手法として、Stochastic Gradient Descent(SGD)を利用する。SGDによる最適化は、予測値と誤差の値を計算して、次の重みの勾配を計算するというわけだ。
# Instantiate the trainer object to drive the model training learning_rate = 0.5 lr_schedule = C.learning_rate_schedule(learning_rate, C.UnitType.minibatch) learner = C.sgd(z.parameters, lr_schedule) trainer = C.Trainer(z, (loss, eval_error), [learner])
さらに、いくつかトレーニングの進捗を確認するための関数群を用意しておく。
# Define a utility function to compute the moving average sum. # A more efficient implementation is possible with np.cumsum() function def moving_average(a, w=10): if len(a) < w: return a[:] return [val if idx < w else sum(a[(idx-w):idx])/w for idx, val in enumerate(a)] # Defines a utility that prints the training progress def print_training_progress(trainer, mb, frequency, verbose=1): training_loss, eval_error = "NA", "NA" if mb % frequency == 0: training_loss = trainer.previous_minibatch_loss_average eval_error = trainer.previous_minibatch_evaluation_average if verbose: print ("Minibatch: {0}, Loss: {1:.4f}, Error: {2:.2f}".format(mb, training_loss, eval_error)) return mb, training_loss, eval_error
トレーニングの実行
ここでは、25個のサンプルを一つのminibatch_sizeとしてトレーニングを実施し、20000個の値に対してトレーニングを実施する。ここで、もし10000個しかデータが存在しない場合、同一のトレーニングを2回実施する。
# Initialize the parameters for the trainer minibatch_size = 25 num_samples_to_train = 20000 num_minibatches_to_train = int(num_samples_to_train / minibatch_size) # Run the trainer and perform model training training_progress_output_freq = 50 plotdata = {"batchsize":[], "loss":[], "error":[]} for i in range(0, num_minibatches_to_train): features, labels = generate_random_data_sample(minibatch_size, input_dim, num_output_classes) # Specify input variables mapping in the model to actual minibatch data to be trained with trainer.train_minibatch({feature : features, label : labels}) batchsize, loss, error = print_training_progress(trainer, i, training_progress_output_freq, verbose=1) if not (loss == "NA" or error =="NA"): plotdata["batchsize"].append(batchsize) plotdata["loss"].append(loss) plotdata["error"].append(error)
Minibatch: 0, Loss: 0.8454, Error: 0.48
Minibatch: 50, Loss: 0.2030, Error: 0.16
Minibatch: 100, Loss: 3.4171, Error: 0.60
Minibatch: 150, Loss: 0.8732, Error: 0.32
Minibatch: 200, Loss: 0.2916, Error: 0.12
Minibatch: 250, Loss: 0.1891, Error: 0.08
Minibatch: 300, Loss: 0.2029, Error: 0.08
Minibatch: 350, Loss: 0.3956, Error: 0.16
Minibatch: 400, Loss: 0.2349, Error: 0.08
Minibatch: 450, Loss: 0.8095, Error: 0.24
Minibatch: 500, Loss: 0.8910, Error: 0.36
Minibatch: 550, Loss: 0.3185, Error: 0.20
Minibatch: 600, Loss: 0.8056, Error: 0.24
Minibatch: 650, Loss: 0.0492, Error: 0.00
Minibatch: 700, Loss: 0.9879, Error: 0.28
Minibatch: 750, Loss: 0.3846, Error: 0.12
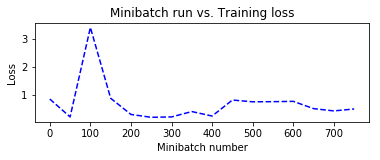
# Compute the moving average loss to smooth out the noise in SGD plotdata["avgloss"] = moving_average(plotdata["loss"]) plotdata["avgerror"] = moving_average(plotdata["error"]) # Plot the training loss and the training error import matplotlib.pyplot as plt plt.figure(1) plt.subplot(211) plt.plot(plotdata["batchsize"], plotdata["avgloss"], 'b--') plt.xlabel('Minibatch number') plt.ylabel('Loss') plt.title('Minibatch run vs. Training loss') plt.show() plt.subplot(212) plt.plot(plotdata["batchsize"], plotdata["avgerror"], 'r--') plt.xlabel('Minibatch number') plt.ylabel('Label Prediction Error') plt.title('Minibatch run vs. Label Prediction Error') plt.show()

評価とテスト
最後に、トレーニングを実施したネットワークに対してデータを入力して評価を行う。新しいデータを生成して、平均誤差と損失を計算する。
これにはtrainer.test_minibatchを使用する。
# Run the trained model on newly generated dataset test_minibatch_size = 25 features, labels = generate_random_data_sample(test_minibatch_size, input_dim, num_output_classes) trainer.test_minibatch({feature : features, label : labels}) out = C.softmax(z) result = out.eval({feature : features}) print("Label :", [np.argmax(label) for label in labels]) print("Predicted:", [np.argmax(result[i,:]) for i in range(len(result))]) # Model parameters print(mydict['b'].value) bias_vector = mydict['b'].value weight_matrix = mydict['w'].value # Plot the data import matplotlib.pyplot as plt # given this is a 2 class colors = ['r' if l == 0 else 'b' for l in labels[:,0]] plt.scatter(features[:,0], features[:,1], c=colors) plt.plot([0, bias_vector[0]/weight_matrix[0][1]], [ bias_vector[1]/weight_matrix[0][0], 0], c = 'g', lw = 3) plt.xlabel("Scaled age (in yrs)") plt.ylabel("Tumor size (in cm)") plt.show()
Label : [1, 1, 0, 0, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 1, 0, 1, 1, 0, 0]
Predicted: [1, 1, 0, 0, 0, 1, 1, 0, 1, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 1, 0, 1, 1, 0, 0]
[ 7.92942953 -7.92942286]